Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 2.Problemas - Ex. 142

O tanque de água na Figura P2.142 tem de largura normal ao papel. Se ele é acelerado para a direita em movimento de corpo rígido a , calcule (a) a profundidade da água no lado e (b) a força causada pela pressão da água sobre o painel . Considere que não haja derramamento.

Passo 1

Fala pessoal!! Vem comigo resolver mais uma questão!!

(a) Para encontramos o resultado pedido, podemos começar usando a seguinte formula para achar o ângulo de inclinação da água dentro do tanque.

Por relação trigonométrica, a partir do esquema feito abaixo

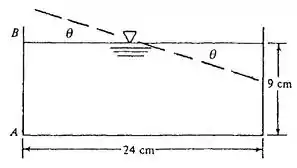
podemos dizer o seguinte:

Logo, a profundidade da água no lado é

Passo 2

(b) A pressão da água em varia linearmente devido à gravidade apenas, portanto, a força da água é

Portanto, a força exercida pela água no lado é de

Resposta

(a)

(b)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um acelerômetro barato, que provavelmente vale pelo que custa, pode ser feito com um tubo em U , como na Figura P2.150. Se L = 18c m e D = 5m m , qual será a altura h se a x = 6m / s 2 ? As marcações

Para que rotação uniforme em rpm em torno do eixo C o tubo em U da Figura P2.155 assumirá a configuração mostrada? O fluido é o mercúrio a 20 ℃ ℃.

Um vaso muito alto com 10c m de diâmetro contém 1.178c m 3 de água. Quando sua rotação é aumentada uniformemente para atingir a rotação de corpo rígido, aparece uma área seca de 4c m de diâmetro no fu

Considere que o tubo em U da Figura P2.150 não é transladado, mas sim rotacionado em torno do seu ramo direito a 95r p m . Qual será o nível h no ramo esquerdo se L = 18c m e D = 5m m ?

Um cilindro aberto de 16c m de diâmetro e 27c m de altura está cheio de água. Calcule a rotação de corpo rígido em torno do seu eixo central, em r p m , (a) para a qual 1 / 3 da água será derramada pa