Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 11.Problemas - Ex. 105

Água fria c p = 4180 J k g . K conduzida a uma ducha entra em um trocador de calor de tubo duplo com parede fina em contracorrente a 15°C, a uma taxa de 0,25 kg/s, e é aquecido a 45°C com água quente c p = 4190 J k g . K ) que entra a 100°C a uma taxa de 3 kg/s. Considerando que o coeficiente global de transferência de calor é 950 W m 2 K , determine a taxa de transferência de calor e a área da superfície de transferência de calor do trocador de calor usando o método ε - N T U .

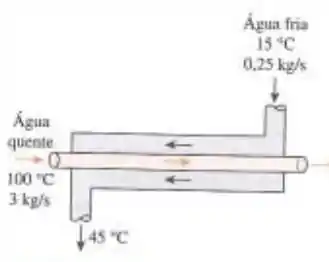
Passo 1

Bora continuar??

A transferência de calor real através deste trocador de calor pode ser descoberta calculando o calor absorvido pela água fria:

Q ˙ = C f T f ,   s a i - T f ,   e n t r a

Já sabemos que:

T f ,   e n t r a = 15 ° C

T f ,   s a i = 45 ° C

Então nós só precisamos do C f . Lembrando que:

C = m ˙ c p

Então:

C q = m a g u a ,   q ˙ c p , q

C f = m a g u a , f ˙ c p , f

Sabendo que:

m a g u a ,   f ˙ = 0,25 k g s

c p , f = 4180   J k g . K

m a g u a , q ˙ = 3 k g s

c p , q = 4190 J k g . K

Substituindo:

C q = 3 k g s 4190 J k g . K = 12570   J s . K = 12570   W K

C f = 0,25 k g s 41 8 0 J k g . K = 1045   J s . K = 1045   W K

Preparados para achar a taxa de transferência de calor?

Q ˙ = 1045   W K 45 ° C - 15 ° C

Q ˙ = 31350   W

Bom, já achamos uma resposta, mas ainda precisamos da área superficial, certo?

Passo 2

Para encontrar a resposta para a segunda pergunta podemos usar a relação:

A s = N T U C m i n U

Já sabemos que:

U = 950 W m 2 K

Para avaliar C m i n vamos ver qual é o menor dentre os valor de C que achamos no Passo 1:

C m a x = C q = 12570   W K

C m i n = C f = 1045   W K

Então a única coisa que nós não temos é o NTU!!

Nestes casos o NTU é calculado como:

N T U = 1 C - 1 . ln ⁡ ε - 1 ε C - 1    

Achar o C é moleza né?

C = C m i n C m a x

Substituindo:

C = 1045   W K 12570   W K = 0,0 83

Passo 3

Para calcular a eficácia nós precisamos lembrar que ele é dado por:

ε = Q ˙ Q m a x ˙

Só precisamos achar o valor máximo de transferência de calor:

Q m a x ˙ = C m i n T q ,   e n t r a - T f ,   e n t r a

Se:

T q ,   e n t r a = 100 ° C

T f ,   e n t r a = 1 5 ° C

C m i n = 1045   W K

Então:

Q m a x ˙ = 1045   W K 100 ° C - 15 ° C

Q m a x ˙ = 88825   W

Na fórmula da eficácia:

ε = 31350   W 88 825   W = 0,35

Agora nós conseguimos calcular o NTU:

N T U = 1 0,083 - 1 . ln ⁡ 0,35 - 1 0,35 0,083 - 1

N T U = 0,438

Passo 4

Na fórmula do Passo 2:

A s = 0,438 1045   W K 950 W m 2 K

A s = 0,4818   m ²

Gostaram dessa ?!

Resposta

Q ˙ = 31350   W     |     A s = 0,4818   m ²

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Água fria ( c p = 4,18k J / k g · K ) entra em um trocador de calor de escoamento cruzado a 14 ℃ ℃, a uma taxa de 0,35k g / s , e é aquecida por ar quente ( c p = 1,0k J / k g · K ) que entra no troca
A água ferve a 150 ℃ ℃ em uma caldeira por gases quentes ( c p = 1,05k J / k g · K ) que entram na caldeira a 540 ℃ ℃, a uma taxa de 0,4k g / s , e a deixam a 200 ℃ ℃.A superfície do trocador de calor
A água de um lago é utilizada como agente de resfriamento em uma termoelétrica.Para conseguir a condensação de 3,2k g / s de vapor saindo da turbina, é usado um trocador de calor de casco e tubo que p
Um condensador resfriado a ar é utilizado para condensar isobutano em uma usina geotérmica binária.O isobutano é condensado a 85 ℃ ℃ por ar ( c p = 1,0k J / k g · ℃ ) ℃ que entra a 22 ℃ ℃, a uma taxa
Um trocador de calor contracorrente é utilizado para resfriar óleo ( c p = 2,20k J / k g · K ) de 110 ℃ ℃ para 85 ℃ ℃ a uma taxa de 0,75k g / s com água fria ( c p = 4,18k J / k g · K ) que entra no t