Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 12.Exercício - Ex. 20

Ar escoa isentropicamente num conduto divergente. A pressão e a temperatura na seção (1) são, respectivamente 0,34 Mpa (abs) e 27ºC e a velocidade é 312 m/s. Se A 2 A 1 = 2,37 , determinar a pressão, a temperatura e a velocidade na seção (2).

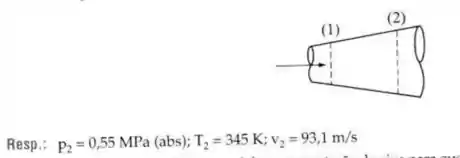
Passo 1

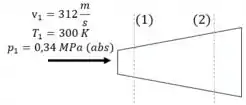
Para calcular as propriedades no ponto (2), precisamos das propriedades de estagnação. Vamos usar os dados que possuímos do ponto (1) para calcular as propriedades de estagnação.

A velocidade de propagação na entrada é:

c 1 = k R T 1 = 1,4 ⋅ 287 ⋅ 300 = 347,19 m s

Podemos calcular o número de Mach:

M 1 = v 1 c 1 = 312 347,19 = 0,9

Agora podemos usar a tabela 1:

T 1 T 0 = 0,8606 ⇒ T 0 = 300 0,8606 = 349   K

p 1 p 0 = 0,5913 ⇒ p 0 = 0,34 0,5913 = 0,574   M P a   ( a b s )

A 1 A * = 1,009

Passo 2

Para conseguir as relações para o ponto (2), vamos relacionar as áreas. Observe que:

A 2 A * = A 2 A 1 ⋅ A 1 A *

Aplicando os valores:

A 2 A * = 2,37 ⋅ 1,009

A 2 A * = 2,39

Agora podemos usar tabela 1 para encontrar as demais relações:

M 2 = 0,25

A temperatura é:

T 2 T 0 = 0,988 T 2 = 0,988 T 0 T 2 = 0,988 ⋅ 349 T 2 = 345   K

A pressão é:

p 2 p 0 = 0,957 p 2 = 0,957 p 0 p 2 = 0,957 ⋅ 0,575 p 2 = 0,55   M P a   ( a b s )

Finalizamos a questão calculando a velocidade:

v 2 = M 2 k R T 2 v 2 = 0,25 ⋅ 1,4 ⋅ 287 ⋅ 345 v 2 = 93,1 m s

Resposta

T 2 = 345   K

p 2 = 0,55   M P a   ( a b s )

v 2 = 93,1 m s

Ver Outros Exercícios desse livro