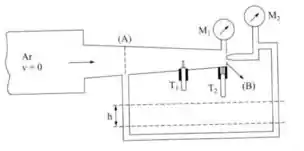
O reservatório da figura é de grandes dimensões e o escoamento no convergente é isentrópico. Determinar:
- A pressão e a temperatura de estagnação;
- A leitura do manômetro quando o tubo de Pitot é instalado na seção (A);
- A velocidade na seção (B)
- A área da seção crítica;
- O desnível h do mercúrio (
Dados:
Passo 1
Dados da questão:
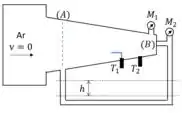
Passo 2
Observe que o termômetro 1 e o manômetro 2 são equipamentos que medem o ponto de estagnação. Então:
Passo 3
O manômetro 2 sempre mede a pressão de estagnação, não importa em que ponto esteja instalado. Além disso, ao longo do escoamento não há maquinas, turbinas ou qualquer outra coisa que cause perda ou ganho de energia no fluxo. Assim, a pressão de estagnação é constante ao longo de todo o fluxo.
Passo 4
Para podermos calcular a velocidade, precisamos da temperatura e número de Mach no ponto (B). O termômetro 2 nos dá o valor da temperatura na seção (B). Como possuímos o valor da temperatura de estagnação, podemos utilizar a tabela 1 para determinar o número de Mach e descobrir a velocidade.
Utilizando a tabela 1, o número de mach é:
Agora podemos calcular a velocidade em B
Passo 5
Ainda na tabela 1 podemos determinar a relação entre a área da seção e a área crítica:
Isolando a área crítica:
Passo 6
O desnível de mercúrio é causado pela pressão no ponto A. Para calcular esta pressão, vamos usar a relação entre a área da seção A e a área crítica:
Agora podemos usar a tabela 1 para determinar a pressão:
Finalizamos utilizando as equações da estática para determinar a altura da coluna de mercúrio: