Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 13.Problemas - Ex. 25
Ar, escoando isentropicamente através de um bocal convergente, descarrega para a atmosfera. Em uma seção, A = 0,05 m², T = 3,3 °C e V = 200 m/s. Se o escoamento está bloqueado, determine a pressão e o número de Mach nessa seção. Qual é a área de garganta? Qual é a vazão mássica?
Passo 1
Beleza! Vamos começar esse exercício calculando o número de Mach na seção 1, então, teremos:
E, como o enunciado nos disse que o escoamento está bloqueado, então, o número de Mach na garganta é:
E então, a pressão é a pressão atmosférica:
Agora, com o auxílio da tabela E.1 do apêndice E, temos para :
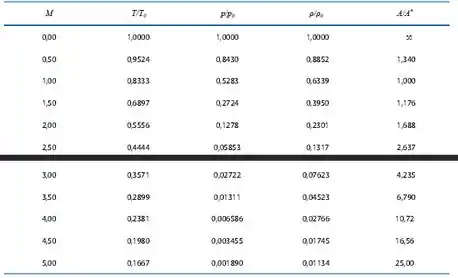
Então a pressão de estagnação será:
Passo 2
Agora, com a pressão de estagnação e as propriedades da seção 1, podemos encontrar as propriedades de interesse, só que para isso, precisamos antes ir novamente na tabela apresentada no passo 1 e encontrar as relações , e para , então, teremos:
Então, para a pressão na seção 1, teremos:
Agora, a temperatura será:
E a área crítica será:
E, como o bocal é convergente e o escoamento é bloqueado, então a área crítica será igual à área da garganta, dessa forma, temos:
Passo 3
Agora, com a pressão encontrada no passo 2, podemos encontrar a densidade do escoamento nessa seção, que será:
E, agora temos todos os dados necessários para encontrar a vazão mássica, que será: