Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 13.Problemas - Ex. 17

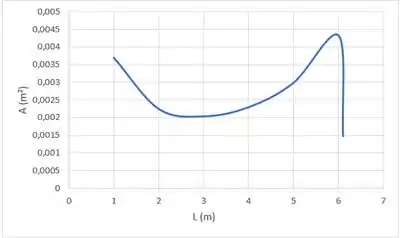
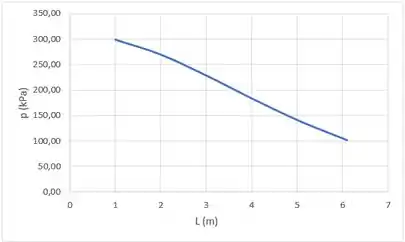
Um canal é projetado para expandir ar isentropicamente até a pressão atmosférica, a partir de um grande tanque no qual as propriedades são mantidas constantes em 5,3 °C e 310 kPa. A vazão desejada é 1kg/s. Considerando que a passagem tem 6,1m de comprimento e que o número de Mach aumenta linearmente com a posição no canal, trace o gráfico da área da seção transversal e da pressão como funções da posição.

Passo 1

A partir do enunciado, têm-se os seguintes dados:

R = 287   N ⋅ m / k g ⋅ K ;

k = 1,4 ;

T 0 = 278,3   K ;

p = 310   k P a ;

p 0 = 101   k P a ;

m ˙ = 1   k g / s .

Calculando M:

p p 0 = 1 + k - 1 2 ⋅ M 2 k / k - 1

310 101 = 1 + 1,4 - 1 2 ⋅ M 2 1,4 1,4 - 1

M = 1,37

Passo 2

Como p 0 p < 0,58 , então, o fluxo é bloqueado.

m ˙ b l o q u e a d o = 0,04 ⋅ A * ⋅ p T 0  

A * = 1,34 × 10 - 3   m 2

Passo 3

A partir do valor de A*, calcula-se o valor de A:

A A * = 1 M ⋅ 1 + k - 1 2 ⋅ M 2 k + 1 2 k + 1 2 k - 1

A = 1,73 × 10 - 3   m 2

Passo 4

Como é dito que o número de Mach aumenta linearmente, e, temos o valor de M = 1,37 para o comprimento de L = 6,1   m . Para o comprimento de L = 1   m , teremos o valor de M = 0,225 . A partir destes valores, calcularemos novos valores de A e p.

Para um novo p 0 , com M = 0,225 : p p 0 = 1 + k - 1 2 ⋅ M 2 k / k - 1

p 0 = 299,26   k P a

Passo 5

Com o novo p 0 , calcula-se a nova A * e A.

m ˙ b l o q u e a d o = 0,04 ⋅ A * ⋅ p 0 T 0  

A * = 1,39 × 10 - 3   m 2

A A * = 1 M ⋅ 1 + k - 1 2 ⋅ M 2 k + 1 2 k + 1 2 k - 1

A = 3,685 × 10 - 3   m 2

Passo 6

Os valores encontrados são:

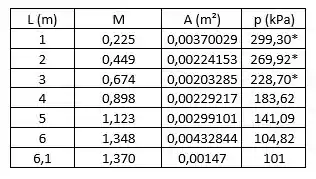
Os valores da tabela com asterisco são momentos em que a relação p / p 0 é maior que 0,58, assim, não possuindo um fluxo mássico bloqueado.

Resposta

G r á f i c o s

Ver Outros Exercícios desse livro