Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 13.Problemas - Ex. 172

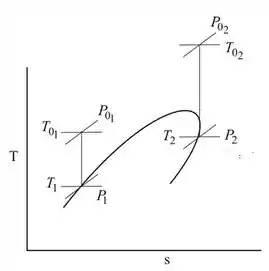
Ar, proveniente do sistema de admissão de um avião, entra na câmara de combustão do motor, onde calor é adicionado durante um processo sem atrito em um tubo de área constante igual a 0,01   m 2 . A temperatura de estagnação isentrópica local e o número de Mach na entrada do combustor são 427   K e 0,3 , respectivamente. A vazão mássica é 0,5   k g / s . Quando a taxa de adição de calor é ajustada em 404   k w , o escoamento sai da câmara de combustão a 1026   K e 22,9   k P a   ( a b s ) . Determine para esse processo: (a) o número de Mach na saída do combustor, (b) a pressão estática na entrada do combustor e (c) a variação na pressão de estagnação isentrópica local durante o processo de adição de calor. Mostre os pontos dos estados de estagnação e estáticos e indique o caminho do processo em um diagrama T s .

Passo 1

Calculando T 1 :

T 0 1 T 1 = 1 + k - 1 2 M 1 2

Sendo:

T 0 1 = 427   K ;

k = 1,4 ;

M 1 = 0,3 .

Temos:

427 T 1 = 1 + 1,4 - 1 2 ⋅ 0,3 2

T 1 = 419,4   K

Calculando T 0 2 :

Q ˙ = m ˙ c p ∆ T = m ˙ c p ( T 0 2 - T 0 1 )

Sendo:

m ˙ = 0,5   k g / s ;

c p = 1004   J / k g ⋅ K ;

Q ˙ = 404   k w .

Temos:

404 x 10 3 = 0,5 ⋅ 1004 ⋅ ( T 0 2 - 427 )

T 0 2 = 1231   K

Calculando T * :

T 0 1 T * = 2 k + 1 M 1 2 1 + k - 1 2 M 1 2 1 + k M 1 2 2

Substituindo:

427 T * = 2 ⋅ 1,4 + 1 ⋅ 0,3 2 1 + 1,4 - 1 2 ⋅ 0,3 2 1 + 1,4 ⋅ 0,3 2 2

T * = 1231   K

Passo 2

Letra a)

Calculando M 2   :

T 1 T 2 = T 1 T * T 2 T * = M 1 1 + k 1 + k M 1 2 M 2 1 + k 1 + k M 2 2 2

T 1 T 2 = M 1 M 2 1 + k M 2 2 1 + k M 1 2 2

Sendo:

T 2 = 1026   K .

Temos:

419,4 1026 = 0,3 M 2 ⋅ 1 + 1,4 ⋅ M 2 2 1 + 1,4 ⋅ 0,3 2 2

M 2 = 0,715 e M 2 = 0,999

Sabendo que T 0 2 é aproximadamente igual a T * , temos então:

M 2 = 0,999 ≅ 1

Passo 3

Letra b)

Calculando p 1 :

p 1 p 2 = p 1 p * p 2 p * = 1 + k 1 + k M 1 2 1 + k 1 + k M 2 2

p 1 p 2 = 1 + k M 2 2 1 + k M 1 2  

Sendo:

p 2 = 22,9   k P a .

Temos:

p 1 22,9 = 1 + 1,4 ⋅ 1 2 1 + 1,4 ⋅ 0,3 2  

p 1 = 48,8   k P a

Passo 4

Letra c)

Calculando p 0 1 :

p 0 1 p 1 = 1 + k - 1 2 M 1 2   k k - 1

Substituindo:

p 0 1 48,8 = 1 + 1,4 - 1 2 ⋅ 0,3 2   1,4 1,4 - 1

p 0 1 = 51,9   k P a

Calculando p 0 2 :

p 0 2 p 2 = 1 + k - 1 2 M 2 2   k k - 1

Substituindo:

p 0 2 22,9 = 1 + 1,4 - 1 2 ⋅ 1 2   1,4 1,4 - 1

p 0 2 = 43,3   k P a

Calculando a variação na pressão de estagnação:

p 0 1 - p 0 2 = 51,9 - 43,3

p 0 1 - p 0 2 = 8,6   k P a

Passo 5

Mostre os pontos dos estados de estagnação e estáticos e indique o caminho do processo em um diagrama T s .

Resposta

M 2 = 1

p 1 = 48,8   k P a

p 0 1 - p 0 2 = 8,6   k P a

Ver Outros Exercícios desse livro