Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 12.Exercício - Ex. 45
Ar quente é retirado de uma sala que contém um forno, para manter um reservatório aquecido. A ligação entre a sala e o reservatório é feita por um convergente/divergente (isoentropico) seguindo de um conduto de seção constante (adiabático com atrito). No reservatório estão instalados um termômetro, um manômetro e ventilador que mantem o regime permanente. Determinar a leitura do manômetro, a leitura do termômetro e a vazão em massa.
Dados:
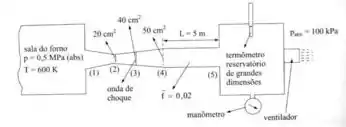
Passo 1
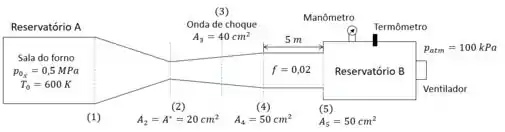
Note que o Reservatório B é de grandes dimensões, então ao atingir o reservatório B o fluxo atinge uma condição de estagnação! Ou seja, a leitura do termômetro e manômetro são iguais a temperatura e pressão de estagnação.
Mas perceba que em (3) ocorre uma onda de choque. À jusante de uma onda de choque a temperatura de estagnação continua a mesma, mas a pressão de estagnação à muda:
Passo 2
Precisamos determinar as propriedades à jusante, então vamos usar a região da onda de choque onde podemos usar as propriedades à montante para determinar propriedades à jusante.
Pela tabela 1 podemos calcular o número de Mach imediatamente à montante da onda de choque.
Com o número de Mach à montante poderemos determinar duas coisas úteis: o número de mach à jusante e a pressão de estagnação à jusante:
Calculamos a pressão de estagnação à jusante:
E como definimos no passo anterior:
Passo 3
Nós possuímos o valor da área para a seção (4), então se obtivermos o valor da área crítica à jusante poderemos determinar as propriedades desta seção. Perceba que não podemos fazer isso para a seção (5), pois a seção (5) NÃO faz parte da região convergente/divergente.
Então como vamos calular as propriedades de (5)? Nós vamos utilizar a equação do escoamento com atrito 12.95 e a Tabela 3.
Passo 4
Agora vamos usar o número de Mach à jusante para determinar a área crítica à jusante.
Passo 5
Agora que temos a área crítica a jusante podemos determinar o número de Mach e a relação de pressão em (4)
Com o número de Mach em (4) vamos para a Tabela 3:
Passo 6
Primeiro vamos calcular a pressão em (4)
E calculamos a pressão crítica:
Passo 7
Para usar a equação 12.95 nós iremos precisar do diâmetro da seção.
E agora aplicamos a Equação 12.95 para encontrar dados sobre a seção (5)
Passo 8
Podemos pegar o valor da perda de carga em (5) e aplicar na Tabela 3
Com o número de Mach podemos determinar a temperatura
Para calcular a vazão vamos precisar do valor da densidade. E para calcular a densidade precisamos do valor da pressão
Podemos calcular a velocidade:
Finalmente, podemos calcular a vazão: