Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 12.Exercício - Ex. 41

No esquema da figura, determinar T 2 ,   p 2 e v 2 Dados: M 1 = 0,5 ; p 1 = 0,14   M P a   a b s e M 2 = 1

Passo 1

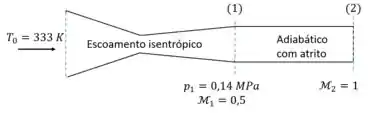
Vamos usar a Tabela 1 e no ponto (1) para determinar a pressão de estagnação do escoamento:

M 1 = 0,5 ⇒ T a b e l a   1 p 1 p 0 1 = 0,843

E calculamos a pressão de estagnação:

p 1 p 0 1 = 0,843

p 0 1 = p 1 0,843

p 0 1 = 0,14 0,843

p 0 1 = 0,166   M P a

Passo 2

Agora vamos para a Tabela 3 e no ponto (1) para determinar a pressão crítica de estagnação do escoamento:

M 1 = 0,5 ⇒ T a b e l a   3 p 0 1 p 0 * = 1,34

E calculamos a pressão crítica de estagnação:

p 0 1 p 0 * = 1,34

p 0 * = p 0 1 1,34

p 0 * = 0,166 1,34

p 0 * = 0,124   M P a

Passo 3

Bom, agora que temos valores do escoamento, podemos utilizá-los para encontrar as propriedades do ponto (2). Observando a Tabelas 1:

M 2 = 1 ⇒ T a b e l a   1 T 2 T 0 = 0,8333 p 0 2 p 0 * = 0,5283

Determinamos a temperatura:

T 2 T 0 = 0,8333

T 2 = 0,8333 ⋅ T 0

T 2 = 0,8333 ⋅ 333

T 2 = 277   K

Determinamos a pressão:

p 0 2 p 0 * = 0,5283

p 0 2 = 0,5283 p 0 *

p 0 2 = 0,5283 ⋅ 0,124

p 0 2 = 0,0655   M P a

Passo 4

Finalizamos a questão calculando a velocidade em (2)

v 2 = M 2 k R T 2

v 2 = 1 ⋅ 1,4 ⋅ 287 ⋅ 277

v 2 = 331,8 m s

Resposta

T 2 = 277   K

p 0 2 = 0,0655   M P a

v 2 = 331,8 m s

Ver Outros Exercícios desse livro