Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 7.Exercício - Ex. 5

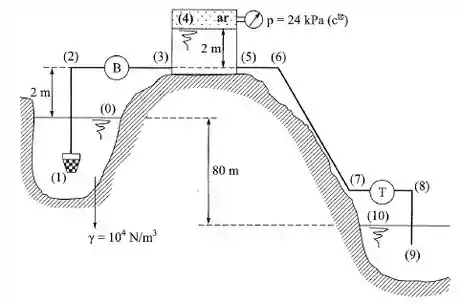
Um motor elétrico fornece 3 kW à bomba da instalação da figura, que tem um rendimento de 80%. Sendo dados:

a) as tubulações são de mesma seção, cujo diâmetro é de 5 cm e de mesmo material;

b) k s 1 = 10 ; k s 2 = k s 8 = 1 ; k s 3 = k s 5 = k s 6 = k s 7 = k s 9 = 0,5 ;

c) a vazão em volume na instalação é de 10 L/s;

d) o comprimento (real) de (1) a (3) é de 10 m, e, de (5) a (9), de 100 m.

Determinar:

a) a perda de carga entre (0) e (4) (total);

b) o coeficiente de perda de carga distribuída;

c) a perda de carga entre (4) e (10) (total);

d) a potência da turbina, sabendo que seu rendimento é de 90%;

e) o comprimento equivalente das singularidades da instalação.

Passo 1

Vamos começar esse exercício calculando a carga da bomba através da fórmula de sua potência:

N B = γ Q H B η B → H B = N B η B γ Q

Substituindo os valores conhecidos, temos:

H B = 3.10 3 0,8 10 4 10.10 - 3 → H B = 24   m

Agora vamos aplicar o equilíbrio de energia entre os pontos 0 e 4:

H 0 + H B = H 4 + H p 0,4

v 0 2 2 g + p 0 γ + z 0 + H B = v 4 2 2 g + p 4 γ + z 4 + H p 0,4

Substituindo os valores conhecidos:

0 2 2 g + 0 γ + 24 = 0 2 2 g + 24.10 3 10 4 + 4 + H p 0,4 → H p 0,4 = 17,6   m

Passo 2

Agora, sabemos que a perda de carga no sistema é a soma da perda distribuída h f mais as perdas localizadas h s , então, podemos escrever a perda de carga como:

H p 0,4 = h f 1,3 + ∑ 1 3 h s → H p 0,4 = f L 1,3 v 2 2 g D H + v 2 2 g ∑ 1 3 k s

Vamos precisar do valor da velocidade, então, através da vazão fornecida e do diâmetro da tubulação, temos:

Q = v A → v = Q A = Q π D 2 4 = 10.10 - 3 π 0,05 2 4 → v = 5,1   m / s

Agora vamos encontrar o valor da perda localizada:

v 2 2 g ∑ 1 3 k s = 5,1 2 2 10 10 + 1 + 0,5 → v 2 2 g ∑ 1 3 k s = 15   m

Agora podemos retornar à equação de perda de carga e isolar f :

H p 0,4 = f L 1,3 v 2 2 g D H + v 2 2 g ∑ 1 3 k s → f = 2 g D H L 1,3 v 2 H p 0,4 - v 2 2 g ∑ 1 3 k s

Substituindo os valores conhecidos, temos:

f = 2 10 0,05 10 5,1 2 17,6 - 15 → f = 0,01

Passo 3

Agora para calcular a perda de carga entre (4) e (10) vamos aplicar a fórmula para a perda de carga vista no passo 2:

H p 4,10 = h f 5,9 + ∑ 5 9 h s → H p 4,10 = f L 5,9 v 2 2 g D H + v 2 2 g ∑ 5 9 k s

Podemos usar o mesmo f encontrado no passo 2, pois o fluido e a geometria do tubo são iguais, então, substituindo os valores conhecidos, temos:

H p 4,10 = 0,01 100 5,1 2 2 10 0,05 + 5,1 2 2 10 0,5 + 0,5 + 0,5 + 1 + 0,5 → H p 4,10 = 29,9   m

Passo 4

Agora, para encontrar a potência da turbina, precisamos primeiro encontrar sua carga, faremos isso aplicando o equilíbrio de energia entre os pontos 4 e 10:

H 4 - H T = H 10 + H p 4,10

v 4 2 2 g + p 4 γ + z 4 - H T = v 10 2 2 g + p 10 γ + z 10 + H p 4,10

Agora, substituindo os valores conhecidos:

0 2 2 g + 24.10 3 10 4 + 84 - H T = 0 2 2 g + 0 γ + 0 + 29,9 → H T = 56,5   m

Agora sim podemos encontrar a potência da turbina (vamos considerar a vazão constante pois o esquema do enunciado nos disse que p 4 deve ser constante, e para isso, não pode haver alteração do nível do fluido nesse reservatório):

N T = η T γ Q H T = 0,9 10 4 10.10 - 3 56,5 → N T = 5085   W = 5,1   k W

Passo 5

O comprimento equivalente das singularidades da estação pode ser encontrado igualando as fórmulas para a perda distribuída e a perda localizada:

h f = h s → f L e q v 2 2 g D H = v 2 2 g ∑ k s

Simplificando a expressão e isolando L e q , temos:

L e q = D H f ∑ k s

Substituindo os valores conhecidos, temos:

L e q = 0,05 0,01 10 + 1 + 1 + 5 0,5 → L e q = 72,5   m

Resposta

H p 0,4 = 17,6   m

f = 0,01

H p 4,10 = 29,9   m

N T = 5,1   k W

L e q = 72,5   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Numa certa região, há três reservatórios naturais, A, B e C, e um conjunto TB formado por uma turbina acoplada diretamente a uma bomba. As perdas de carga nas tubulações são:Entre a e b, H p a , b = 0
Calcular a vazão na tubulação da figura para H = 10m . Calcular em seguida o novo valor de H para que a vazão seja 50L / s . Dados: D = 150m m ;ν = 1,05.10 - 6m 2 / s ; γ = 10 4N / m 3 ; k = 25,9.10 -
Dada a instalação da figura, determinar a pressão p 0 para que a vazão seja 6 L/s. Em seguida, traçar a linha piezométrica e a linha de energia sobre a instalação, marcando o valor das respectivas alt
Água escoa em regime laminar num conduto cilíndrico horizontal de diâmetro D. A linha de energia forma com a horizontal um ângulo α . Determinar a vazão. Dados: ν = 10 - 6m 2 / s ; D = 1c m ; tg ⁡ α =
Na instalação da figura, a bomba B recalca uma vazão Q e a LE para tal vazão tem a configuração indicada. A tubulação tem diâmetro constante D = 25m m e o coeficiente de perda de carga f = 0,025 . Sab