Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 6º - Capítulo 13.Problemas - Ex. 51

Um arranho para a conversão direta de energia térmica e, energia elétrica é mostrada na figura. O cilindro interno, com diâmetro D 1 = 25 m m , é aquecido internamente por um processo de combustão que leva o cilindro de cerâmica ( ε i = 0.9 ) a uma temperatura superficial de T i = 1675 ° C . O cilindro externo, com diâmetro D e = 0.38   m , é feito com um material semicondutor ( ε e = 0.5 ) que converte a irradiação incidente absorvida em corrente elétrica. O material que serve de base para o semicondutor é um metal altamente condutor que é resfriado com água para 20°C. O conversador é considerado muito longo quando comparado ao diâmetro externo. Há vácuo no espaço entre os dois cilindros concêntricos.

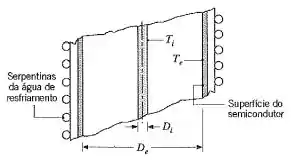
Supondo superfícies cinza e difusas, determine a taxa de transferência de calor por unidade de área do cilindro externo. A saída elétrica da superfície do semicondutor é de 10% da irradiação absorvida na região com comprimentos de onda entre 0,6   e   2,0   μ m . Para as condições especificadas, determine a geração de energia em watts por unidade de área da superfície externa.

Passo 1

Falaaaa moçadinha, show de bola?

Como diz o Homem de ferro “Eu tenho um plano. Ataque!”

Bora atacar esse problemaaaaaaa junto comigoo.

Os dados fornecidos são

Diâmetro interno do cilindro D i = 25   m m = 0.025   m

Raio interno do cilindro, r i = 0.125   m

Diâmetro externo do cilindro, D o = 0.38   m

Raio externo do cilindro r o = 0.19   m

Emissividade do cilindro ε 0 = 0.5

Temperatura interna T i = 1675 ° C  

Emissividade externa do cilindro, ε 0 = 0.5

Temperatura externa do cilindro, T o = 20 ° C = 293 K

Suposições

  1. Duas superfícies são invólucros.
  2. As superfícies são cinzentas e difusas.

Passo 2

  1. A troca liquida de radiação da área da superfície externa

    2. q i o = A i σ T i 4 - T o 4 1 ε i + 1 - ε o ε o r i r o

    Aonde

    A i = 2 π r i l é a área interna

    A o = 2 π r o l é a área externa

    A i A o = r i r o

    = 0.0125 0.19

    = 0.066

    Passo 3

    A troca liquida de radiação por unidade de área da superfície externa

    q i o A o = A i A o σ T i 4 - T o 4 1 ε i + 1 - ε o ε o r i r o

    = 0.066 5.78 × 10 - 8 1948 4 - 293 4 1 0.9 + 1 - 0.5 0.5 0.066

    = 53859.30 1.11 + 0.066

    q i o A o = 45.8   k W / m 2

    Passo 4

  2. A geração de energia por unidade de área de superfície A o

p e ' ' = n e F a b s ( 0.6 → 20 μ m )

Onde

A irradiação total

G a b s = ε i o A o

p e ' ' = n e q i o A o F 0 → 2 μ m - F 0 → 0.6 μ m

Partindo da tabela

T = 2 T i

= 2 1948

= 3896   μ m K

Ver o fator 0 a 2 μ m

  F 0 → 2 μ m = 0.461

Ver o fator 0 a 0.6 μ m

F 0 → 0.6 μ m = 0.0019

p e ' ' = 0.1 45.8 0.461 - 0.0019

p e ' ' = 2.1   k W / m 2

“Às vezes é preciso aprender a correr antes de começar a andar”

Resposta

  1. q i o A o = 45.8   k W / m 2

p e ' ' = 2.1   k W / m 2

Exercícios de Livros Relacionados

Como a radiosidade é definida para uma superfície? Para superfícies difusamente emissoras e refletoras, como a radiosidade está́ relacionada com a intensidade da radiação emitida e refletida?
A superfície escura do topo de um fogão cerâmico pode ser aproximada por um corpo negro. Os “queimadores”, que estão integrados ao topo do fogão, são aquecidos por baixo por aquecedores de resistência
A distribuição espectral da radiação emitida por uma superfície difusa pode ser aproximada como segue.(a) Qual é o poder emissivo total? (b) Qual é a intensidade total da radiação emitida na direção n
Uma pequena placa plana está posicionada logo após a atmosfera terrestre e encontra-se orientada de modo que sua normal passa pelo centro do Sol. Utilize o Problema 12.20 para obter as dimensões perti