Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 12.Problemas - Ex. 19

A superfície escura do topo de um fogão cerâmico pode ser aproximada por um corpo negro. Os “queimadores”, que estão integrados ao topo do fogão, são aquecidos por baixo por aquecedores de resistência elétrica.

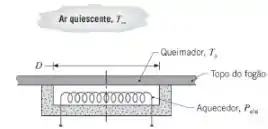
(a) Considere um queimador com diâmetro   D   =   200   m m operando com uma temperatura na superfície uniforme de T s   =   250 ° C em ar ambiente a T ∞   =   20 ° C . Sem um pote ou panela sobre o queimador, quais são as taxas de perda térmica por radiação e por convecção no queimador? Sendo a eficiência associada à transferência de energia dos aquecedores para os queimadores de 90 % , qual é a exigência de potência elétrica? Em qual comprimento de onda a emissão espectral é um máximo?

(b) Calcule e represente graficamente o efeito da temperatura do queimador nas taxas de transferência de calor para 100   ≤   T s   ≤   350 ° C .

Passo 1

Vamos passar um raio X nessa questão? Aqui nós temos o diâmetro e temperatura do queimador, temperatura do ar ambiente e eficiência do queimador.

Com isso, queremos encontrar as taxas de calor por radiação e convecção e comprimento de onda correspondentes à emissão espectral máxima e a taxa de consumo de energia elétrica, show? Então vamos lá!

Passo 2

Para resolver essa questão vamos assumir que:

(1) O queimador emite como corpo negro;

(2) A Irradiação desprezível do queimador do ambiente;

(3) O ar ambiente é inativo;

(4) As propriedades são constantes.

Para emissão de um corpo negro,

q r a d = A s E b = π D 2 4 σ T 4 = π 0,2 m 2 4 5,67 × 10 - 8 W m 2 . K 4 523   K 4 = 133   W

Com,

L = A s P = D 4 = 0,05 m

E,

R a L = g β ( T s - T ∞ ) L 3 α ν = 6,35 × 10 5

h - = k L N u L - = k L 0,54   R a L 1 / 4 = 10,5 w m 2 . K

Passo 3

Então,

q c o n v = h - A s T s - T ∞ = 10,5 W m 2 . K π 0,2 m 2 4 230   K = 75,7   W

E o requisito de energia elétrica é então,

P e l e c = q r a d + q c o n v η = 133 + 75,7 W 0,9 = 232   W

Já o comprimento de onda correspondente ao pico de emissão é obtido pela lei de deslocamento de Wien é,

λ m a x = 2898   μ m . K 523   K = 5,54   μ m

Resposta

  1. q r a d = 133   W ,               q c o n v = 75,7   W ,         P e l e c = 232   W     e           λ m a x = 5,54   μ m
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere uma pequena superfície com área A 1=10 – 4 m 2 , que emite difusamente com um poder emissivo hemisférico total de E 1=5×10 4W / m 2 . (a) A que taxa essa emissão é interceptada por uma peque
Qual é a irradiação nas superfícies A 2 ,A 3 e A 4 do Exemplo 12.1 devido à emissão a partir de A 1 ?
De acordo com sua distribuição direcional, a radiação solar que incide sobre a superfície terrestre pode ser dividida em duas parcelas. A parcela direta, que é constituída por raios paralelos que inci
Uma pequena fonte de calor radiante com área A 1= 2×10 – 4m 2 emite difusamente com uma intensidade I 1=1000W / ( m 2 · s r ) . Uma segunda área pequena,A 2=1 ×10 – 4m 2 está localizada como mostrado
Em um dia encoberto, a distribuição direcional da radiação solar que incide na superfície terrestre pode ser aproximada por uma expressão com a forma I i=I nc o s ( θ ) , sendo I n=80W / ( m 2 · s r )