Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 13.Problemas - Ex. 86

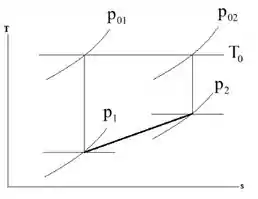
Um avião supersônico voa a M = 2,7 a uma altitude de 18000   m . Um choque normal ocorre em frente a um tubo de pitot sobre o avião; o tubo mede a pressão de estagnação de 72   k P a   a b s . Calcule a pressão estática e a temperatura atrás do choque. Avalie a perda na pressão de estagnação através do choque. Determine a variação na entropia específica através do choque. Mostre os estados de estagnação e estáticos e o caminho do processo em um diagrama T s .

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Primeiro, temos que assumir algumas hipóteses:

  • Escoamento isoentrópico, estável e uniforme;
  • Ar como gás ideal;

Vamos considerar as seguintes equações:

P 0 P = 1 + k - 1 2 M 2 k k - 1

T 0 T = 1 + k - 1 2 M 2

E:

∆ s = c p ln ⁡ T 2 T 1 - R ln ⁡ P 2 P 1

Para altitude de 18   k m na tabela A . 3 , tem-se que:

T 1 = 216,7   K

R = 2 96,8 J k g ⋅ K

k = 1,4

Temos também que:

P 1 = 7,25   k P a

P 1 P 01 = 0,04295

Portanto:

P 01 = 168,8   k P a

O número de Mach na saída será:

M 2 = 0,7837

Passo 2

Substituindo os dados na primeira equação, temos que:

P 02 P 01 = 0,4236

Logo:

P 02 = 71,5   k P a

Substituindo os dados na segunda equação, temos que:

T 2 T 1 = 2,343

A temperatura após o choque é de:

T 2 = 507,7   K

Passo 3

Substituindo, novamente, os dados na primeira equação, temos que:

P 2 P 1 = 8,338

A pressão estática após o choque é de:

P 2 = 60,45   k P a

Considerando que a temperatura não muda durante o choque, o aumento da entropia está relacionado apenas à perda da pressão de estagnação, portanto:

∆ s = 1004 ln ⁡ 1 - 286,9 ln ⁡ 8,33

∆ s = 286,9 ln ⁡ 8,33

Logo, o valor da variação de entropia para as condições impostas é dado por:

∆ s = 608,4 N ⋅ m k g ⋅ K

O diagrama T s é dado abaixo:

Resposta

T 2 = 507,7   K

P 2 = 60,45   k P a

∆ s = 608,4 N ⋅ m k g ⋅ K

Ver Outros Exercícios desse livro