Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 12.Problemas - Ex. 50
Um avião supersônico voa a 3 km de altitude a uma velocidade de 1000 m/s em um dia-padrão. Quanto tempo após o avião passar diretamente acima de um observador que está no solo o seu som é ouvido pelo observador?
Passo 1
Oi pessoal, tudo bem?
Para o esboço do que é descrito no problema, temos:
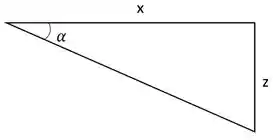
Então, podemos dizer que:
Consideremos:
Obs: Propriedades do ar (Tabela A.6). ;
A temperatura é encontrada na tabela A.3 com base na altitude do avião.
Passo 2
Sabemos que a velocidade do som:
E que o M depende da velocidade do som, de modo que:
Primeiramente, a velocidade do som:
Portanto, o número de Mach é:
Como o depende do deslocamento , precisamos encontrar o valor do ângulo de Mach, dado por:
Então:
Passo 3
Porém, a nível do mar, a velocidade do som será diferente daquela a 3km de altitude, devido à diferença de temperatura, e afetará o tempo para que o observador ouça o avião. A temperatura à nível do mar é dada por , aproximadamente. Assim, a velocidade do som:
Portanto, o número de Mach é:
Como o depende do deslocamento , precisamos encontrar o valor do ângulo de Mach, dado por:
Então:
Resposta
Portanto, sabemos que o som alcança o observador entre 8,62s e 8,29s. Fazendo uma média, podemos destacar que o som alcança o observador em 8,55s.