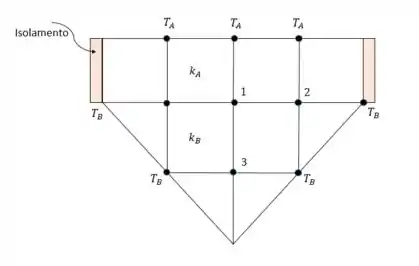
Uma barra bidimensional tem geometria, mostrada na Fig. P5-128, com temperatura especificada T A sobre a superfície superior e T B sobre a superfície inferior e isolamento nas laterais. A condutividade térmica da parte superior da barra é k A , enquanto a da parte inferior é k B . Para uma malha definida por ∆ x = ∆ y = l , escreva a forma mais simples da matriz de equações A T = C , usada para determinar o campo de temperatura permanente na seção transversal da barra. Identifique na figura os nós da malha onde você irá escrever o balanço de energia.

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 5.Problemas - Ex. 128

Uma barra bidimensional tem geometria, mostrada na Fig. P5-128, com temperatura especificada sobre a superfície superior e sobre a superfície inferior e isolamento nas laterais. A condutividade térmica da parte superior da barra é , enquanto a da parte inferior é . Para uma malha definida por , escreva a forma mais simples da matriz de equações , usada para determinar o campo de temperatura permanente na seção transversal da barra. Identifique na figura os nós da malha onde você irá escrever o balanço de energia.

Passo 1

Primeiramente, iremos assumir algumas considerações para simplificar o problema. São elas:

A transferência de calor através do corpo é bidimensional e em regime permanente.
A condutividade térmica é constante.
Não há geração de calor.

De posse dessas características, e sabendo que existe um eixo de simetria na figura e três temperaturas desconhecidas nos nós centrais e , podemos entender melhor o sistema com o qual a questão pretende trabalhar.

Passo 2

A formulação de diferenças finitas fica da seguinte maneira:

Nó :

Passo 3

A matriz de equações fica da seguinte maneira:

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro