Reconsidere o Prob. 5-126. A absorção da radiação solar, neste caso, pode ser expressa de forma mais exata como polinômio do quarto grau como:

Onde é o fluxo solar incidente na superfície do lago, em , e é a distância a partir da superfície livre do lago em . Resolva o Prob. 5-126 utilizando essa relação para absorção da radiação solar.

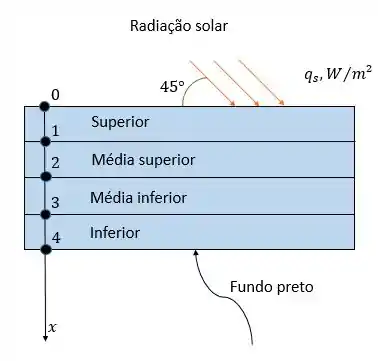
A radiação solar incidente em uma grande massa de água limpa ( e ) como lago, rio ou lagoa é, na maior parte, absorvida pela água, e a quantidade absorvida varia de acordo com a profundidade. Para radiação solar incidente em ângulo de em um grande lago de de profundidade cuja superfície inferior é preta (refletividade zero), por exemplo, da energia solar é refletida de volta para a atmosfera, é absorvida pela superfície inferior e o restante é absorvido pela água. Se o lago é considerado como tendo quatro camadas de igual espessura (, neste caso), pode ser demonstrado que da energia solar incidente é absorvida pela camada superior, pela camada média superior, pela camada média inferior e pela camada inferior. A radiação absorvida pela água pode ser tratada convenientemente como sendo geração de calor, na análise de transferência de calor do lago.

Considere um grande lago de de profundidade, inicialmente a uma temperatura uniforme de . A energia solar incide a sobre a superfície do lago a uma taxa média anual de durante o período de quatro horas. Pressupondo que não haja correntes de convecção na água e utilizando o método explícito de diferenças finitas com tamanho de malha de e passo de tempo , determine a distribuição de temperatura no lago sob as condições mais favoráveis (ou seja, não há perdas de calor a partir da superfície superior ou inferior do lago). A energia solar absorvida pela superfície no fundo do lago pode ser tratada como fluxo de calor para água na superfície, neste caso.

O espaçamento nodal é de , então a quantidade de nós é . Então, temos um problema envolvendo temperaturas nodais desconhecidas, então precisaremos de equações para descobri-las. Os nós e são interiores, então podemos utilizar a formulação explícita de diferenças finitas, expressa como:

Onde a variável de interesse é , q é a temperatura na localização do nó interior. O nó também pode ser analisado como um nó interior pelo conceito de imagem do espelho, e o nó tem a sua equação de diferenças finitas obtida à partir de um balanço energético, seguindo as direções de transferências de calor que vão para o nó.

Nó 0:

Nó 1:

Nó 2:

Nó 3:

Nó 4:

O número de Fourier pode ser calculado com os dados que o problema fornece:

Entretanto, a radiação solar agora obedece à uma lei dada por um polinômio do quarto grau, então calcula-se o valor da geração de calor para cada nó substituindo-se o valor de correspondente:

E o fluxo de calor na superfície superior:

E as propriedades da água limpa são dadas no problema, logo, após substituição nas equações vistas em cada nó no passo , tém-se a distribuição de temperaturas desejada para cada ponto nodal do lago.