Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 5.Problemas - Ex. 129

Uma barra longa de aço tem seção transversal mostrada na Fig. P5-129. A barra é removida do forno de tratamento térmico a T i = 700 ℃ e colocada no fundo de um tanque cheio de água a 10 ℃ . Para intensificar a transferência de calor, a água é vigorosamente circulada, gerando temperatura constante de praticamente T s = 10 ℃ em todos os lados da barra, exceto na parte inferior, que é adiabática. As propriedades da barra são C p = 430   J / k g . K ,   k = 40   W / m . K   e   ρ = 8000 k g / m ³ .

(a) Escreva as equações de diferenças finitas para temperaturas desconhecidas na malha, utilizando o método explícito. Agrupe todas as quantidades no termo constante. Identifique parâmetros adimensionais como Bi e Fo, se for o caso.

(b) Determine o intervalo do passo de tempo onde o método explícito é numericamente estável.

(c) Para ∆ t = 10 s , determine o campo de temperatura em t = 10 s e t = 20 s . Preencha o quadro a seguir:

Passo 1

Primeiramente, iremos assumir algumas considerações para simplificar o problema. São elas:

  • A transferência de calor através do corpo é bidimensional e em regime transiente
  • Todas as superfícies da barra, exceto a superfície inferior, são mantidas constantes a T s = 10 ℃ .
  • A condutividade térmica k é constante.
  • Não há geração de calor.

De posse dessas características, podemos entender melhor o sistema com o qual a questão pretende trabalhar.

Passo 2

(a) A formulação de diferenças finitas para as temperaturas desconhecidas ficam da seguinte maneira:

Nó 5 :

k T 7 i -   T 5 i ∆ x ∆ x + k T 6 i -   T 5 i ∆ x ∆ x + k T 2 i -   T 5 i ∆ x ∆ x + k T 4 i -   T 5 i ∆ x ∆ x =   ρ C p ∆ x ² T 5 i + 1 -   T 5 i ∆ t

T 7 i +   T 6 i +   T 2 i + T 4 i - 4 T 5 i = ρ C p ∆ x ² T 5 i + 1 -   T 5 i k ∆ t

  T 5 i + 1 =   T 5 i 1 - 4 F o + F o T 2 i + 30 F o

Sabendo que T 7 i =   T 6 i =   T 4 i = 10 ℃ e F o =   k ∆ t / ρ C p ∆ x ² .

Nó 2 :

k T 1 i -   T 2 i ∆ x ∆ x 2 + k T 5 i -   T 2 i ∆ x ∆ x + k T 3 i -   T 2 i ∆ x ∆ x 2 =   ρ C p ∆ x ² 2 T 2 i + 1 -   T 2 i ∆ t

T 1 i +   2 T 5 i +   T 3 i - 4 T 2 i = ρ C p ∆ x ² T 2 i + 1 -   T 2 i k ∆ t

  T 2 i + 1 =   T 2 i 1 - 4 F o + 2 F o T 5 i + 2 0 F o

Passo 3

(b) A condição de estabilidade para ambos os nós é igual, sendo calculada da seguinte maneira:

1 - 4 F o ≥ 0 → F o ≤ 1 4 → k ∆ t / ρ C p ∆ x ² ≤ 1 4

∆ t ≤ ρ C p ∆ x 2 4 k = 8000 × 430 × 0,025 2 4 × 40 → ∆ t ≤ 13,44 s

Passo 4

(c) Para ∆ t = 10 s :

F o =   k ∆ t / ρ C p ∆ x 2

F o =   40 × 10 8000 × 430 × 0,025 ² = 0,186  

E utilizando esse valor na equação de cada nó, temos:

T 5 i + 1 =   0,256 T 5 i + 0,186 T 2 i + 5,58

T 2 i + 1 = 0,256 T 2 i + 0,372 T 5 i + 3,72

Para ∆ t = 10 s , ainda estamos dentro da estabilidade do sistema, logo T 5 i =   T 2 i =   T i = 700 ℃ , então:

T 5 1 =   0,256 700 + 0,186 700 + 5,5 8 = 315 ℃  

T 2 1 = 0,256 700 + 0,372 700 + 3,72 = 443,3 ℃

E para ∆ t = 20 s , utilizam-se os valores do passo anterior:

T 5 2 =   0,256 315 + 0,186 443,3 + 5,58 = 168,6 ℃

T 2 2 = 0,256 443,3 + 0,372 315 + 3,72 = 234,4 ℃

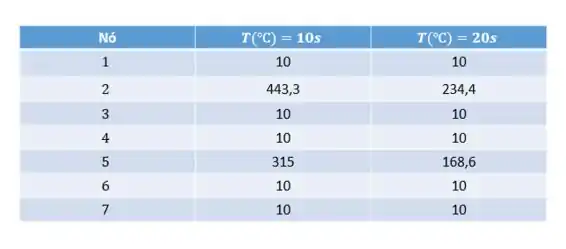
E preenchendo a tabela inicial, temos:

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro