Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 12.Exercício - Ex. 36
No bocal da figura escoa ar (. Numa certa condição, a seção de área mínima é crítica, a massa específica na seção (1), de área é e o escoamento até essa seção é isentrópico. Variando a pressão a jusante, obteve-se uma segunda situação, ocorrendo uma onda choque na seção (1). Para a segunda situação, determinar:
- A temperatura a montante da onda de choque
- A vazão em massa;
- e na garganta.
Passo 1
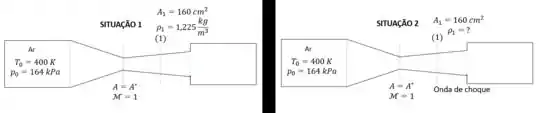
Item A)
Primeiro vamos considerar primeiro a SITUAÇÃO 1!
Como não houve onda de choque, sabemos que o escoamento em (1) é subsônico
Vamos usar as propriedades de estagnação para calcular a densidade de estagnação:
Agora podemos usar a razão entre as densidades para trabalhar com a Tabela 1.
Agora vamos pensar na SITUAÇÃO 2!
As áreas são fixas, então a relação entre elas continuam as mesmas. Mas agora houve uma onda de choque, ou seja, o escoamento é supersônico!
Agora é só calcular a temperatura à montante:
Passo 2
Item B)
Vamos continuar trabalhando a SITUAÇÃO 2.
Vamos calcular a pressão à montante na situação 2:
Agora vamos calcular a densidade do fluxo utilizando a lei dos gases:
E calculamos a velocidade do fluxo:
E agora finalizamos o item calculando a vazão mássica da situação 2:
Passo 3
A garganta é o ponto crítico, logo:
Vamos usar isso para determinar a temperatura da garganta:
Com a temperatura podemos calcular a velocidade