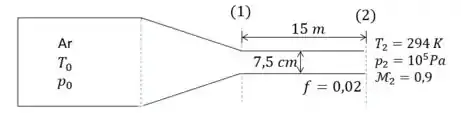
O ar de um reservatório escoa por um tubo isolado termicamente de diâmetro interno e comprimento de . Na saída, as condições são e . Adota-se que o coeficiente de perda de carga distribuída seja 0,02 constante. Supondo o escoamento isentrópico e continuo desde o reservatório até o tubo isolado, determinar a temperatura e a pressão de estagnação no reservatório.

Vamos pegar os valores necessários na Tabela 3:

E agora podemos calcular os valores críticos:

Reorganizando a Equação 12.95

Substituindo os valores:

Com esse valor, vamos voltar à tabela 3

Pela Tabela 3

Como já temos os valores críticos, podemos calcular as propriedades do ponto (1)

Utilizando o valor do Número de Mach podemos usar a Tabela 1 para determinar as propriedades de estagnação:

A temperatura no reservatório é:

A pressão no reservatório é: