Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Operações Unitárias - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 11.Problemas - Ex. 58

A bomba para água modelo A-12251 da Worthington Corp., operando no ponto de máximo rendimento, produz 16,2 m de altura de carga a 3.550 rpm, consome 1,1 hp de potência de eixo a 3.200 rpm, e fornece 3,8 l/s a 2.940 rpm. Que tipo de bomba é esse? Qual é o seu rendimento e como ele se compara com o da Figura 11.14? Calcule o diâmetro do rotor.

Passo 1

E aí, galera, tudo bem? MecFlu pode parecer difícil, mas cola aqui que eu vou te ajudar!

Nessa questão, temos uma bomba operando no ponto de máximo rendimento fornece uma altura de carga H = 16,2   m a uma rotação angular n 1 = 3550   r p m = 59,2   r p s , consome uma potência de P = 1,1   h p = 0,820   k W a n 2 = 3200 e fornece uma vazão de Q = 3,8   L / s = 0,0038   m 3 / s a n 3 = 2940 .

O enunciado nos pede então pra descobrir o tipo da bomba, seu rendimento e pra calcular o diâmetro do rotor.

Nos próximos passos eu vou te ensinar a calcular tudo isso, mas antes de ir pro Passo 2, mas antes nós temos que lembrar que a massa específica da água a 20 ° C é ρ = 998   k g / m ³ .

Agora sim, vem comigo pra gente matar esse problema juntos!

Passo 2

Pra começar a questão, vamos calcular a potência P * e a vazão Q * na mesma rotação que produz a altura de carga de 16,2   m , ou seja, n 1 = 3550   r p m .

Pra isso, vamos usar as leis de semelhança, dadas pelas equações 11.23 (página 777), considerando que o diâmetro se mantém constante.

Primeiro, calculando a nova potência:

P * = P n 1 n 2 3 = 0,820   k W 3550   r p m 3200   r p m 3 = 1,12   k W

Depois, a nova vazão:

Q * = Q n 1 n 2 2 = 0,0038   m 3 / s   3550   r p m 2940   r p m = 0,0046   m 3 / s

Passo 3

Agora podemos calcular a rotação especifica N S a partir da Equação 11.30b (página 784), considerando a rotação n 1 :

N S = n 1 ,   r p m Q ,   m 3 / s 1 / 2 H ,   m 3 / 4

N S = 3550   r p m 0,0046   m 3 / s 1 / 2 16,2   m 3 / 4

N S = 29,8

Como N S = 27,2 está entre 10 e 80, a teoria nos diz que essa bomba é centrífuga.

Passo 4

Nesse passo, vamos calcular o rendimento máximo para a rotação de n 1 = 3550   r p m :

η m á x = ρ g Q * H P *

η m á x = 998   k g / m ³ 9,81   m / s ² 0,0046   m 3 / s 16,2   m 1,12   k W

η m á x = 65,1 %

Se a gente entrar com o valor de Q * e N S na Figura 11.14 (páginan787), a gente consegue comparar e ver que os valores pra η m á x são muito parecidos:

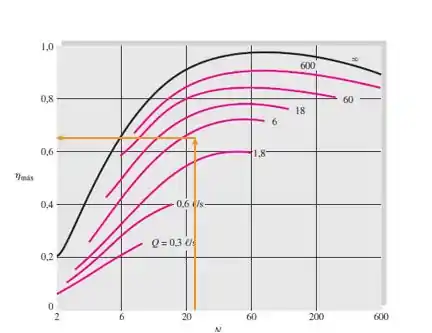
Passo 5

Agora pra finalizar a questão vamos resolver calcular o diâmetro do rotor D .

Primeiro vamos na Figura P11.49, onde podemos encontrar o coeficiente adimensional de vazão C Q * pra uma bomba centríguga:

Logo, C Q * ≈ 0,085 .

A gente tem que lembrar também que temos uma expressão pra C Q * pela Equação 11.23 (página 777):

C Q * = Q * n 1 D ³

Igualando as duas equações, poderemos resolver e encontrar D :

0,0046   m 3 / s 59,2   r p s D ³ = 0,085

D = 0,097   m

Pronto, matamos a questão juntos!

Resposta

A bomba é centrífuga, tem rendimento η m á x = 65,1 % e o seu rotor tem um diâmetro de D = 0,097   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma bomba típica de poço doméstico fornece uma vazão de 0,31l / s contra uma altura de carga de 4,6m . Com 1.750r p m , qual tipo de bomba você recomenda?
Determine as rotações específicas dos sete rotores das bombas Taco, Inc., da Figura P11.24. Elas são apropriadas para projetos centrífugos? Elas são aproximadamente iguais dentro da incerteza experime
Os dados coletados pelo autor para o coeficiente de potência no PMR de 30 bombas diferentes são traçados em função da rotação específica na Figura P11.50. Determine se os valores de C P * para as três
Uma bomba comercial opera a 1.750r / m i n e fornece, próximo ao PMR, uma vazão de 145l / s a uma altura de carga de 40m . (a) Qual é o tipo de bomba? (b) Calcule o diâmetro do rotor usando os dados d
A resposta ao Problema P11.40 é que o adimensional “diâmetro específico” tem a forma D s = D g H * 1 4 / Q * 1 2 , calculado no PMR. Dados reunidos pelo autor para 30 bombas diferentes indicam, na Fig