Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 4.Problemas - Ex. 65

Calcule a força requerida para manter o tampão fixo na saído do tubo de água. A vazão é 1,5   m 3 / s e a pressão a montante é 3,5   M P a .

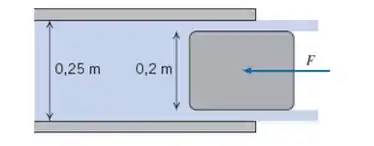
Passo 1

Considerações Iniciais:

  1. Escoamento em estado estacionário;
  2. Escoamento incompressível;
  3. Escoamento com velocidade constante;
  4. Escoamento uniforme.

Passo 2

Primeiramente devemos achar as áreas das duas seções e também suas velocidades.

Para a Seção 1:

A 1 = π D 1 2 4 = π ⋅ 0,25 2 4 = 0,049   m 2

V 1 = Q A 1 = 1,5 0,049 = 30,6   m / s

Para a Seção 2:

Essa seção se dá pelas duas passagens acima e abaixo do tampão.

A 2 = π ⋅ ( D 1 2 - D 2 2 ) 4 = π ⋅ ( 0,25 2 - 0,2 2 ) 4 = 0,0 177   m 2

V 2 = Q A 2 = 1,5 0,0 177 = 84,7   m / s

Passo 3

Pelas considerações feitas no Passo 1, a equação do momento sofre a seguinte transformação:

F S + F B = ∂ ∂ t ∫ V C V ρ d ∀ + ∫ S C V ρ V d A

Como ∂ ∂ t = 0 :

- F + P 1 A 1 - P 2 A 2 = - V 1 ρ V 1 A 1 + V 2 ρ V 2 A 2

Sendo:

P 1 = 3,5   M P a ;

P 2 = 0   P a ;

ρ = 1000   k g / m 3 .

Temos:

- F + 3,5 x 10 6 ⋅ 0,049 - 0 ⋅ 0,0177 = - 30,6 2 ⋅ 1000 ⋅ 0,049 + 84,7 2 ⋅ 1000 ⋅ 0,0177

F = 90,4   k N

Resposta

F = 90,4   k N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Expresse a segunda lei do movimento de Newton para pás rotativas. O que é possível dizer sobre a velocidade angular e o momento angular de um corpo não rígido em rotação de massa constante, se o torqu
Dois bombeiros estão combatendo um incêndio com mangueiras e bocais de água idênticos, exceto que um segura a mangueira em linha reta para que a água saia do bocal na mesma direção em que entra, enqua
Na aplicação da equação do momento, explique por que em geral podemos desprezar a pressão atmosférica e trabalhar apenas com pressões manométricas.
Considere dois corpos rígidos com mesma massa e velocidade angular. Você acha que esses dois corpos devem ter o mesmo momento angular? Explique.
Descreva as forças de corpo e as forças de superfície e explique como a força resultante que age sobre o volume de controle é determinada. O peso do fluido é uma força de corpo ou uma força de superfí