Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 4.Problemas - Ex. 76

Obtenha expressões para a taxa de variação em massa do volume de controle mostrado, bem, como as forças horizontal e vertical requeridas para manter o volume de controle fixo, em função de P 1 ,   A 1 ,   V 1 , P 2 ,   A 2 ,   V 2 ,   P 3 ,   A 3 ,   V 3 ,   P 4 ,   A 4 ,   V 4 e da massa específica constante.

2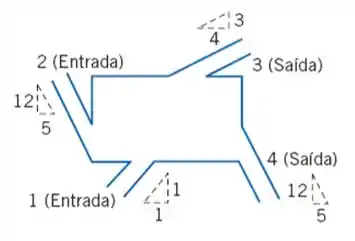

Passo 1

Considerações Iniciais:

  1. Escoamento em estado estacionário;
  2. Escoamento incompressível;
  3. Escoamento com velocidade constante;
  4. Escoamento uniforme.

Passo 2

Pelas considerações feitas no passo 1, utilizaremos equação do balanço de massa para o volume controle:

d m V C d t + ∑ S C ρ A V = 0

Analisando a figura, temos que entradas possuem sinais negativos, já saídas, positivos.

d m V C d t + ρ - A 1 V 1 - A 2 V 2 + A 3 V 3 + A 4 V 4 = 0

A expressão para a taxa de variação em massa do volume de controle mostrado será:

d m V C d t = ρ A 1 V 1 + A 2 V 2 - A 3 V 3 - A 4 V 4

Passo 3

Pela equação da conservação de momento, temos:

F = F S + F B = ∂ ∂ t ∫ V C V ρ   d ∀ + ∫ S C V ( ρ V ) d A

Não temos a variação das propriedades com o tempo nem força de campo atuando, então:

∂ ∂ t = 0

F = F S + F B = ∫ S C V ( ρ V ) d A

Passo 4

Para a componente x :

F x + P 1 A 1 2 + 5 P 2 A 2 13 - 4 P 3 A 3 5 - 5 P 4 A 4 13 = 0 + V 1 - ρ A 1 V 1 2 + 5 V 2 - ρ A 2 V 2 13 + 4 V 3 ρ A 3 V 3 5 + 5 V 4 ρ A 4 V 4 13

Com pressões positivas nas entradas, e negativas nas saídas.

F x = - P 1 A 1 2 - 5 P 2 A 2 13 + 4 P 3 A 3 5 + 5 P 4 A 4 13 + V 1 - ρ A 1 V 1 2 + 5 V 2 - ρ A 2 V 2 13 + 4 V 3 ρ A 3 V 3 5 + 5 V 4 ρ A 4 V 4 13

F x = A 1 2 - P 1 - ρ V 1 2 + 5 13 - P 2 A 2 + P 4 A 4 - ρ A 2 V 2 2 + ρ A 4 V 4 + 4 A 3 5 ( P 3 + ρ V 3 2 )

Passo 5

Para a componente y :

F y + P 1 A 1 2 - 12 P 2 A 2 13 - 3 P 3 A 3 5 + 12 P 4 A 4 13 = 0 + V 1 - ρ A 1 V 1 2 - 12 V 2 - ρ A 2 V 2 13 + 3 V 3 ρ A 3 V 3 5 - 12 V 4 ρ A 4 V 4 13

F y = - P 1 A 1 2 + 12 P 2 A 2 13 + 3 P 3 A 3 5 - 12 P 4 A 4 13 + V 1 - ρ A 1 V 1 2 - 12 V 2 - ρ A 2 V 2 13 + 3 V 3 ρ A 3 V 3 5 - 12 V 4 ρ A 4 V 4 13

F y = A 1 2 - P 1 - ρ V 1 2 + 12 13 P 2 A 2 - P 4 A 4 + ρ A 2 V 2 2 - ρ A 4 V 4 + 3 A 3 5 ( P 3 + ρ V 3 2 )

Resposta

d m V C d t = ρ A 1 V 1 + A 2 V 2 - A 3 V 3 - A 4 V 4

F x = A 1 2 - P 1 - ρ V 1 2 + 5 13 - P 2 A 2 + P 4 A 4 - ρ A 2 V 2 2 + ρ A 4 V 4 + 4 A 3 5 ( P 3 + ρ V 3 2 )

F y = A 1 2 - P 1 - ρ V 1 2 + 12 13 P 2 A 2 - P 4 A 4 + ρ A 2 V 2 2 - ρ A 4 V 4 + 3 A 3 5 ( P 3 + ρ V 3 2 )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Qual a importância do fator de correção do fluxo do momento na análise do momento dos sistemas de escoamento? Para qual tipo de escoamento ele é significativo e deve ser considerando na análise: escoa
Explique a importância do teorema de transporte de Reynolds na mecânica dos fluidos e descreva como a equação do momento linear é obtida a partir dele.
Enuncie a primeira, segunda e terceira leis de Newton.
Um foguete no espaço (nenhum atrito ou resistência ao movimento) pode expelir gases a uma certa velocidade alta V em relação a si mesmo. V é o limite superior para velocidade final do foguete?
Como as forças de superfície surgem na análise do momento de um volume de controle? Como é possível minimizar o número de forças de superfície expostas durante a análise?