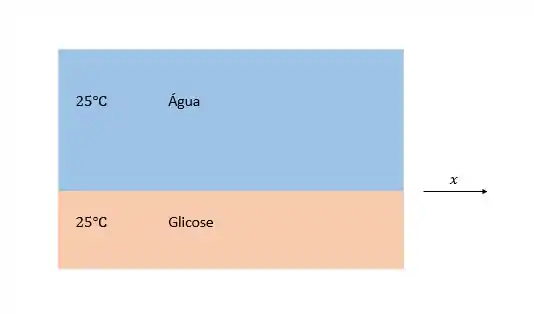
Uma camada de glicose está submersa em uma camada profunda de água a . Como a camada de glicose se dissolve na água, sua densidade na interface água-glicose é mantida constante. Determine o tempo necessário para a concentração de glicose a chegar a de concentração na interface glicose-água.

Primeiramente, iremos assumir algumas considerações para simplificar o problema. São elas:

• A piscina de água pode ser modelada como um meio semi-infinito.
• A concentração de glicose na água é, inicialmente, igual a zero.
• O coeficiente de difusão de glicose na água a é , segundo a tabela 14-3a.

De posse dessas características, podemos entender melhor o sistema com o qual a questão pretende trabalhar.

No capítulo , tivemos um problema análogo a esse, onde havia uma condução de calor unidimensional e transiente em um meio semi-infinito, com temperatura na superfície especificada. Logo, resolvendo de acordo, a solução pode ser expressa como:

Substituindo os valores especificados, temos:

Na tabela 4-4, nós temos o valor da função erro relacionado ao argumento da função erro, ou seja, , então: