Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 10.Problemas - Ex. 30

Um canal de formato V revestido de tijolos de barro, com um ângulo total de 90°, tem 1 km de comprimento e um declive de 1:400. Quando operando a uma profundidade de 2m, a extremidade a montante é fechada repentinamente enquanto a extremidade a jusante continua a drenar. Considerando uma vazão normal quase permanente, determine o tempo para a profundidade do canal baixar para 20 cm.

Passo 1

Fala aí, galera!!! Bora pra mais um “lerigou” da mecânica dos fluidos? Vamos desenhar pra gente entender o que tá sendo dito no enunciado!!!

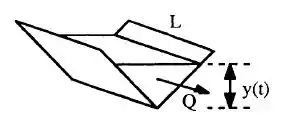
Vamos agora assumir algumas coisas importantes!

O estado quase-estacionário com fluxo uniforme em qualquer instante. Para um volume de controle que possa ter todo o canal com comprimento L = 1km, nós temos o balanço de massa dizendo o seguinte:

d d t m V C = - m ˙ s a í d a

Podemos abrir ainda essa equação de tal forma que temos:

d d t ρ V = - ρ Q s a í d a

d d t L A = - Q s a í d a = - 1 n A R h 2 3 S o 1 2

Passo 2

Para um canal no estilo de “V” como mostrado no desenho, temos que:

A = y 2 c o t θ = y 2 c o t 45 °

R h = y 2 c o s θ = y 2 c o s 45 °

L = 1000   m

S o = 1 400

Passo 3

Vamos agora fazer uma separação de variáveis depois de substituir A, Rh e L, beleza?

∫ y o y d y y 5 3 = - c o n s t ∫ 0 t d t

y o - 2 3 - y - 2 3 = C t

C = 1 n cos ⁡ 45 2 2 3 S 0 3 2 L = 0,00199  

Passo 4

Para o nosso caso, temos:

2 - 2 3 - 0,2 - 2 3 = - 0,00119 t d r e n a g e m

t d r e n a g e m = 1927 s → 32   m i n

Resposta

t = 32   m i n

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Como a inclinação do atrito é definida? Sob quais condições ela é igual à inclinação de fundo de um canal aberto?
Expresse a equação da energia unidimensional para o escoamento de canal aberto entre uma seção a montante 1 e uma seção a jusante 2 e explique como a perda de carga pode ser determinada.
Quando podemos dizer que o escoamento em um canal aberto é uniforme? Sob quais condições o escoamento em um canal aberto permanece uniforme?
A melhor seção transversal hidráulica para um canal trapezoidal com largura de base b é aquela para a qual o comprimento da lateral da seção de escoamento é ( a )b( b )b / 2( c )2 b ou ( d ) .
Água escoa através de um canal retangular com 4m de largura e velocidade média de 5m / s . Se o escoamento é crítico, determine a vazão da água.