Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 10.Problemas - Ex. 27
Um canal circular de concreto sem acabamento para água tem uma declividade de 1:600 e um diâmetro de 1,52 m. Avalie a vazão normal em litros/min para a qual a tensão cisalhante média na parede é 7,18 N/m² e compare o seu resultado com a vazão máxima possível esse canal.
Passo 1
Fala aí, galera!!! Bora pra mais um “lerigou” da mecânica dos fluidos? Vamos desenhhhaaarrrr!!!
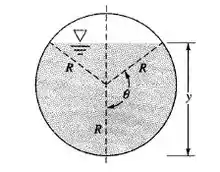
Para um concreto sem acabamento, o valor do coeficiente de rugosidade “n” é de 0,014. De acordo com o livro, a tensão de cisalhamento pode ser obtida como sendo:
Onde
Na equação acima para tensão de cisalhamento, podemos isolar o raio hidráulico para encontrar seu valor e posteriormente substituir ele no raio hidráulico do círculo para encontrar o valor do ângulo, certo?
Passo 2
Resolvendo nossa equação para
Para uma área de
Passo 3
Isso é abaixo do ponto de máxima vazão, a qual ocorre quando , computando a vazão temos:
Isso é em torno de 71% da vazão máxima!