Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 11.Problemas - Ex. 20
Para um canal de seção transversal não retangular, a profundidade crítica ocorre a uma energia específica mínima. Obtenha uma equação geral para a profundidade crítica em um canal de seção trapezoidal em função de , , e . Ela será implícita em !
Passo 1
Vamos visualizar o canal para ficar mais fácil de montar a equação!
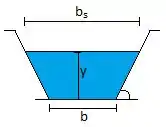
Aeee! Esse é nosso canal, que lindo!
Olhando agora para a fórmula que nos ajuda a encontrar a energia:
Bora reescrever essa equação de outra forma, fazendo aparecer a vazão, como o enunciado nos pediu:
Tá começando a tomar forma, hein? Vamos continuar!
Passo 2
Agora vamos visitar a tabela 11.1, porque nosso enunciado não falou nada sobre área de escoamento, então temos que reescrever esse termo. HÁ tabela nos diz que:
Show! Substituindo isso na nossa equação da energia:
Partiu próximo passo!
Passo 3
A gente não pode esquecer que o exercício quer os fatores críticos, então:
Prontinho! Encontramos a equação geral em função de , , , e com implícito.