Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 13.Problemas - Ex. 62

Um cartucho de C O 2 é usado para propelir um “carrinho foguete”. Gás comprimido, armazenado a 35 MPa e 20ºC, é expandido através de um bocal convergente de contorno suave cuja garganta tem 0,5 mm de diâmetro. A contrapressão é atmosférica. Calcule a pressão na garganta do bocal. Avalie a vazão mássica de dióxido de carbono através do bocal. Determine o empuxo disponível para impulsionar o carrinho. De quanto aumentaria o empuxo, se uma seção divergente fosse acrescentada ao bocal para expandir o gás até a pressão atmosférica? Qual é a área de saída? Mostre os estados de estagnação e estáticos e os processos em um diagrama Ts.

Passo 1

Oi pessoal, tudo bem ?

Consideremos:

  P 0 = 35   M P a         T 0 = 293   K       D = 0,5   m m     |

As propriedades do C O 2 são encontradas na Tabela A.6:   k = 1 , 29       R   = 188,9   J k g K

Devemos lembrar que a vazão mássica através do bocal é dada por:

m ˙ = ρ V A

Passo 2

Caso 1: Afim de descobrir a velocidade de saída do bocal, sabemos que:

V = M c = M k R T

Para a relação isentrópica, a pressão crítica ( M = 1 ) pode ser encontrada através de:

P c r i t = P 0 1 + k - 1 2 k k - 1 = 35 * 10 6 1 + 1,29 - 1 2 1,29 1,29 - 1 =   → P c r i t = 19,2   M P a      

Portanto, a pressão da garganta é igual a pressão crítica; P c r i t = P g .

A temperatura de saída T g é informada por:

T 0 T g = 1 + k - 1 2 M 2   → T g = 293 1 + 1 , 29 - 1 2   = 256   K

Então a velocidade de saída no bocal é:

V = 1 , 29 * 188,9 * 256     → V = 250 m s

E, o ρ g é:

ρ g = P g R T g = 19,2 * 10 6 188,9 * 256 = 3 9 6   k g m 3

Então a vazão mássica é:

  m ˙ = 3 9 6 * 250 * π * 0,05 2 4 * 10 - 6     → m ˙ = 0 , 0194 k g s  

Passo 3

Para a descoberta da força de empuxo, lembremos:

F s x + F b x = ∂ ∂ t ∫ V x ρ d ∀ + ∫ V x

Então, a equação do momento fica:

R x + P g A g = m ˙ V g

R x = m ˙ V e + P g A g       → R x = 8 , 6   N

Passo 4

Caso 2: Se uma seção divergente fosse acrescentada ao bocal para expandir o gás até a pressão atmosférica, não teremos condições críticas. Logo, é necessário descobrir o número de Mach:

Obs: A pressão de saída foi informada igual à atmosférica, então P a t m = P = 101,325   k P a .

M = P 0 P k - 1 k - 1 2 k - 1 1 2 = 35 * 10 6 101,325 * 10 3 1 , 29 - 1 1 , 29 - 1 2 1 , 29 - 1 1 2   →     M = 4 , 34

A temperatura de saída T e é informada por:

T 0 T e = 1 + k - 1 2 M 2   → T e = 293 1 + 1,29 - 1 2 4,34 ²   = 78,7   K

Então a velocidade de saída no bocal é:

V e = 4,34 1,29 * 188,9 * 78,7     → V e = 600 m s

E, o ρ g é:

ρ e = P e R T e = 1 01,325 * 10 3 188,9 * 78,7 = 6,8   k g m 3

Para a nova equação do momento:

R x = m ˙ V e → R x = 11,67   N

Portanto o aumento percentual do empuxo é:

11,67 - 8,6 8,6 = 35,7   %

E a área de saída é:

A e = m ˙ ρ e V e = 0,0194 6,8 * 600   → A e = 4,76 * 10 - 6   m ²

Resposta

Portanto o aumento percentual do empuxo é: 35,7   %

E a área de saída é: A e = 4,76 * 10 - 6   m ²

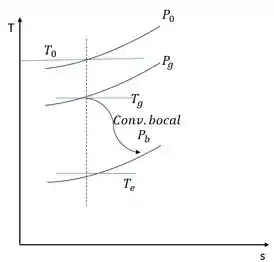
Diagrama T.s:

Ver Outros Exercícios desse livro