Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 6º - Capítulo 1.Problemas - Ex. 58
Células-combustível isoladas, como a do Exemplo 1.4, podem ser escalonadas através de sua organização em uma pilha de células-combustível. Uma pilha é constituída por múltiplas membranas eletrolíticas que são colocadas entre duas placas bipolares eletricamente condutoras. Ar e hidrogénio são alimentados em cada membrana através de canais de escoamento no interior de cada placa bipolar, como mostrado no esquema. Com esta montagem da pilha, as células-combustível individuais estão conectadas eletricamente em série, produzindo uma voltagem na pilha de , onde é a voltagem produzida através de cada membrana e N é o número de membranas na célula. A corrente elétrica é a mesma em cada membrana. A voltagem da célula, assim como a eficiência da célula, aumenta com a temperatura (o ar e o hidrogénio alimentados na pilha são umidificados para permitir a operação em temperaturas superiores a do Exemplo 1.4), porém as membranas irão falhar em temperaturas excedendo . Considere membranas com , e espessura , as quais cada uma produz de energia térmica quando operando a . As superfícies externas da pilha estão expostas ao ar a e à vizinhança a com e .
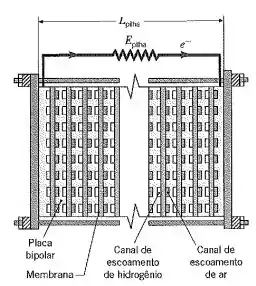
- Encontre a potência elétrica produzida por uma pilha com comprimento de , para espessuras das placas bipolares na faixa de Determine a energia térmica total gerada pela pilha.
- Calcule a temperatura superficial e explique se a pilha necessita ser internamente aquecida ou resfriada para operar na temperatura interna ótima de 80°C para várias espessuras da placa bipolar.
- Identifique como a temperatura interna de operação da pilha pode ser diminuída ou elevada para uma dada espessura da placa bipolar e discuta mudanças no projeto que promoveriam uma distribuição de temperaturas no interior da pilha mais uniforme. Como variações nas temperaturas do ar externo e da vizinhança afetariam a sua resposta? Qual membrana na pilha é mais passível de falha em função de uma alta temperatura de operação?
Passo 1
Falai galerinha, tudo certo:
Como diria a Viúva Negra, “Ainda somos amigos, certo?”
Boraaa fazer essa comigo
Vamos iniciar ela escrevendo a expressão para calcular a potência elétrica pois ela nos será útil, já que a letra (a) solicita que calculemos a potência elétrica produzida por uma pilha, logo:
Passo 2
Agora iremos expressar uma formula para calcular a energia térmica total
Portanto, a energia térmica total é de .
Passo 3
Para a letra (b) vamos começar com a expressão para calcular a área da Pilha
Vamos escrever agora a expressão para calcular o balanço de energia no volume de controle
Vamos substituir os valores numéricos que temos
Portanto, a temperatura da superfície é
A temperatura da superfície e muito maior do que a temperatura operacional ideal. Portanto, a pilha precisa estar refrigerada internamente em condições de operar na temperatura interna ideal de .
Passo 4
Para o calculo da energia térmica da pilha relacionando a condutividade térmica e o comprimento teremos
Vamos escrever agora a formula para a transferência de calor na temperatura interna ótima
Portanto, a taxa de transferência de calor por cada pilha é de
Passo 5
Para finalizar a letra (b) vamos escrever a expressão para calcular a transferência total de calor
Portanto, a transferência líquida de calor pela chaminé é maior que a energia térmica total. Sendo assim, a pilha precisa ser resfriada internamente, para operar na temperatura ideal.
Passo 6
Para a letra (c) vamos expressar a formula para a transferência de calor na temperatura interna ótima
Temos a diferença de temperatura operacional ideal é inversamente proporcional à área.
A temperatura da pilha pode ser diminuída, se a área da seção transversal das placas for maior que . Devido ao aumento da área, a emissividade também aumenta. A temperatura da pilha pode ser aumentada isolando as superfícies da pilha.
As mudanças de projeto que promoveram a temperatura interna uniforme são as seguintes:
Use matérias com alta condutividade térmica
Aumentar a espessura das placas bipolares.
A temperatura operacional da pilha será afetada com uma mudança no ar externo e na temperatura ambiente. Se a temperatura ambiente ou a temperatura do ar aumentar, isso fará com que a temperatura operacional aumente.
A membrana da pilha que experimenta as temperaturas operacionais mais altas terá a alta probabilidade de falha. Mesmo as placas ou membranas bipolares que são finas também podem ter chances de falha.
“Nós somos Groot”
Resposta
Vide a explicação.