Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 7.Problemas - Ex. 42
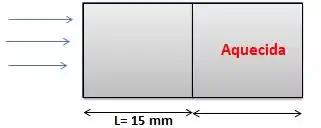
Um chip de silício de 15 mm x 15 mm é montado de tal forma que as bordas estão alinhadas em um substrato. O chip dissipa 1,4 W de potência de maneira uniforme, enquanto o ar a 20°C (1 atm) e velocidade de 25 m/s é usado para resfriar a superfície superior do chip. Se o substrato fornece um comprimento inicial sem aquecimento de 15 mm, determine a temperatura da superfície no bordo de fuga do chip. Avalie as propriedades do ar a 50°C
Passo 1
O enunciado quer que a gente calcule a temperatura no final do substrato, ou seja, em L = 30 mm, e, além disso, perceba que há uma parte não aquecida. Esses dois pontos são muito importantes pra gente calcular a temperatura da superfície no bordo de fuga. Só a gente lembrar que nessa posição o calor sairá na forma de convecção, beleza?
Passo 2
Primeiro a gente tem que saber qual é o regime de escoamento nessa posição, certo?
Ou seja, o escoamento durante toda a placa é laminar
Passo 3
Como temos uma região de não aquecimento, temos uma relação entre o Nusselt associado a essa condição com o Nusselt assiciado como se toda a placa tivesse aquecimento, este último vamos chamar de , onde ξ =0 significa que TODA PLACA É AQUECIDA.
E a relação entre os Nusselts é:
Vamos agora abrir a equação e substituir os valores, se liga!
Passo 4
Agora é só ser feliz pra encontrarmos a temperatura de superfície!
Perceba que a área que aparece nessa equação é a de TROCA TÉRMICA, então vamos considerar apenas a do chip que troca calor com ar.