Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 8.Problemas - Ex. 80
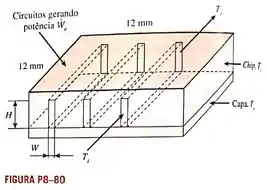
Um chip de silício é resfriado com água que passa através de um microcanal gravado a parte de trás do chip, como mostrado na Fig. P8-70. Os canais são cobertos com tampa de silício. Considere um chip quadrado de com microcanais retangulares gravados, cada um de largura e altura . Água entra nos microcanais a temperatura e vazão total de . O chip e a tampa são mantidos a uma temperatura uniforme de . Considerando que o escoamento nos canais está completamente desenvolvido e que todo calor gerado pelos circuitos na superfície de cima do chip é transferido para a água e usando correlações para tubo circular, determine:
A temperatura de saída da água,
A dissipação de potência do chip,
Passo 1
Dados fornecidos:
Comprimento do chip:
Largura do chip:
Número de microcanais:
Altura do micro canal:
Largura do canal micro:
Temperatura da água de entrada:
Vazão total:
Temperatura uniforme de chip e da tampa:
Passo 2
Podemos obter as propriedades da água da tabela A-9, assumido uma temperatura média para a água de
Calor específico:
Condutividade térmica:
Viscosidade dinâmica:
Densidade:
Número de Prandtl:
Passo 3
a) Para resolver essa questão, primeiro nós temos que encontrar a vazão mássica através de cada canal. Assim temos:
Aqui, é a vazão mássica total, e é o número de microcanais. Substituindo os termos da relação pelos dados fornecidos, temos:
Podemos calcuar a área de seção transversal usando a seguinte relação:
Aqui, é a altura do micro canal, e é a largura do canal micro. Substituindo os termos da relação pelos dados fornecidos, temos:
Passo 4
Agora, vamos calcular o diâmetro hidráulico do microcanal usando a seguinte relação:
Aqui, é o perímetro da seção transversal. Substituindo os termos da relação pelos dados fornecidos, temos:
Podemos calcular a velocidade média do fluxo com a seguinte expressão:
Aqui, é o fluxo mássico, é a área da seção transversal, é a densidade e é a velocidade média. Substituindo os termos da relação pelos dados fornecidos, temos:
Passo 5
Com a velocidade média e o diâmetro hidráulico, podemos calcular o número de Reynolds. Assim temos:
Substituindo os termos da relação pelos dados fornecidos, temos:
Como o número de Reynolds obtido é menor que , o fluxo é laminar.
Passo 6
Podemos então tomar o valor do número de Nusselt da tabela 8-1 “Números de Nusselt para escoamento laminar completamente desenvolvido”, para seção transversal de tubo circular a temperatura da superfície constante como sendo:
Assim, podemos calcular o coeficiente de transferência de calor usando a seguinte relação:
Substituindo os termos da equação pelos dados fornecidos e encontrados, temos:
Podemos calcular a área de superfície de transferência de calor da seguinte maneira:
Passo 7
Agora, podemos então calcular a temperatura de saída usando a seguinte relação:
Aqui é a temperatura do fluxo de entrada, é a temperatura da superfície do tubo, é a temperatura do fluxo de saída, é a área da superfície, o coeficiente de transferência de calor e é a vazão mássica.
Temos que , substituindo temos:
Substituindo os termos pelos dados encontrados anteriormente e fornecidos no enunciado, temos:
Portanto, a temperatura de saída é .
Passo 8
Podemos calcular a taxa de potência dissipada com a seguinte relação:
Onde é dado da seguinte forma:
Substituindo na relação da taxa, temos:
Substituindo os termos pelos dados encontrados anteriormente e fornecidos no enunciado, temos:
Portanto, a dissipação de potência do chip é
Resposta
a)
b)