Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 8.Problemas - Ex. 81
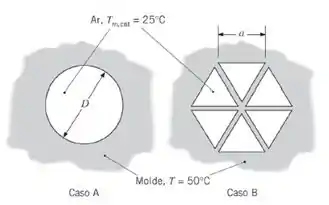
Ar a escoa com uma vazão de através de canais com de comprimento usados para resfriar um molde metálico de alta condutividade térmica. Suponha que o escoamento esteja fluidodinâmica e termicamente plenamente desenvolvido.
(a) Determine o calor transferido para o ar em um canal circular (D = 10 mm), quando a temperatura do molde é de 50°C (caso A).
(b) Usando novos métodos de fabricação (veja o Problema 8.105), canais com seção transversal complexa podem ser facilmente criados no interior de objetos metálicos, como os moldes. Considere o ar escoando nas mesmas condições do caso A, exceto que agora o canal é segmentado em seis seções triangulares menores. A área de escoamento do caso A é igual à área de escoamento total do caso B. Determine o calor transferido para o ar no caso do canal segmentado.
(c) Compare as quedas de pressão nos casos A e B.
Passo 1
Beleza galerinha, vamos lá! (a) O número Reynolds é,
Assim, o fluxo é laminar. Uma vez que também se assumiu que o fluxo está totalmente desenvolvido e a temperatura do molde é uniforme, o número Nusselt é
A temperatura de saída pode ser encontrada na Equação 8.41b,
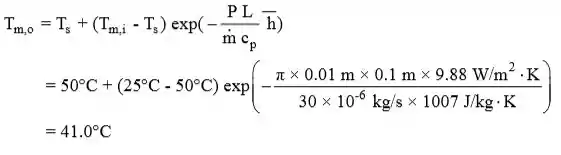
Logo,
Passo 2
(b) Determinamos primeiro as dimensões dos canais triangulares a partir da exigência de que a área total seja a mesma do caso A.
e a vazão em um canal é de . O número Reynolds é,
A temperatura de saída é,
Depois, utilizando a taxa de fluxo total para contabilizar os seis canais,
Passo 3
(c) O fator de atrito para o caso A é f = 64/ReD = 64/202 = 0,317. A queda de pressão é, a partir da Equação 8.22a,
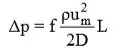
Logo,
Para o caso B, da Tabela 8.1, f = 53/ReD = 53/98.6 = 0,538, e um = 0,339 m/s, como no caso A. Assim,
