Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 12.Problemas - Ex. 13
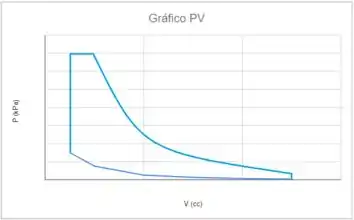
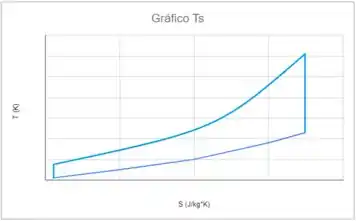
O ciclo de um motor diesel de quatro tempos típico é algumas vezes modelado como um sistema ideal fechado de padrão de ar. Neste sistema simplificado, o processo de combustão é modelado como um processo de aquecimento, e o processo de sucção descarga como um processo de resfriamento do fluido de trabalho (ar). O ciclo consiste em: compressão isentrópica do estado ((abs), , ) para o estado ( ); adição de calor a volume constante (isométrica, isocórica ou isovolumétrica) para o estado 3 (); adição de calor à pressão constante (isobárica) para o estado (); expansão isentrópica para o estado ; e resfriamento a volume constante de volta para o estado . Trace os diagramas e para este ciclo ideal e determine a eficiência, definida como o trabalho líquido (a área delimitada pelo ciclo no diagrama ) dividido pelo calor adicionado.
Passo 1
Vamos começar anotando todos os nossos dados pra gente não se perder, beleza?
Mas a gente não pode esquecer de anotar as nossas constantes, que já estão tabeladas, e que temos que observar que elas apresentam o Kelvin como unidade de temperatura então precisamos ajustar isso aí. Partiu!
Beleza! Vamos começar no próximo passo com os cálculos!
Passo 2
Bom, para o processo nós vamos ter um processo de compressão isentrópica, segundo nosso enunciado, então temos que:
constanteconstante
E assim teremos:
E para achar a pressão:
Agora precisamos calcular o trabalho, para depois montar o diagrama que o exercício pediu, vamos nessa:
E como é isentrópico:
Show! Conseguimos para a primeira parte do processo, agora vamos para a segunda!
Passo 3
Para o processo nós vamos ter um volume constante, segundo nosso enunciado, então temos que:
E agora para achar a pressão:
Se nosso volume é constante nesse processo, então: , vamo achar o agora, beleza?! Partiu!
Opa! Vamos ter que achar esse aí hein?!
Agora podemos voltar na equação do :
Uhul! Agora partiu próximo processo!
Passo 4
Para o processo nós vamos ter a pressão constante, então:
Vamos achar a temperatura primeiro:
Vamos então calcular o trabalho:
Agora podemos voltar na equação do :
Show! Agora o próximo processo!
Passo 5
Para o processo também é isentrópico. E assim teremos:
E para achar a pressão:
precisamos calcular o trabalho:
E o . Show! Partiu último processo!
Passo 6
No último processo, temos o volume constante, então vamos ter:
Se nosso volume é constante nesse processo, então: , vamos achar o agora, beleza?! Partiu!
Agora podemos voltar na equação do :
Passo 7
Aeee! Depois de todos os processos calculados, podemos encontrar o trabalho total:
E encontrando a eficiência:
Partiu encontrar o :
Partiu encontrar o :
Agora sim podemos achar a eficiência:
Agora é só plotar os gráficos!
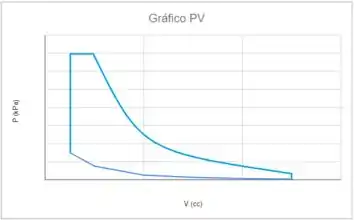
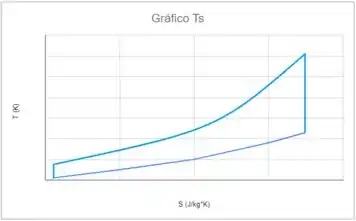
Resposta
