Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 4.Problemas - Ex. 72

Uma comporta possui 1   m de largura e 1,2   m de altura, é articulada no fundo. De um lado, a comporta suporta uma coluna de água com 1   m de profundidade. De outro lado, um jato de água com 5   c m de diâmetro atinge a comporta a uma altura de 1   m . Qual velocidade V é necessária para que o jato mantenha a comporta na vertical? Qual será essa velocidade se a coluna de água for diminuída para 0,5   m ? Qual será a velocidade se a coluna de água for diminuída para 0,25   m ?

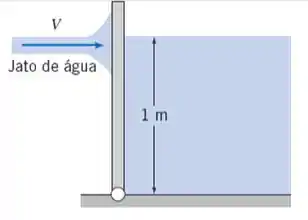
Passo 1

Equação do Momento:

F = F S + F B = ∂ ∂ t ∫ V C V ρ d ∀ + ∫ S C V   ρ V d A

Considerações:

  1. Escoamento Estacionário;
  2. Fluxo Incompressível;
  3. Fluxo Uniforme;
  4. Sem Forças de Corpo Atuando.

Passo 2

Com as considerações do Passo 1, trabalhando no e i x o   y e sabendo que F S = R x , temos:

R x = ∫ S C u   ρ V d A = u ρ ⋅ - u A = - u 2 ρ A

F j a t o - R x = u 2 ρ π D 2 4

Passo 3

Em situações de jatos contra paredes, temos as seguintes equações para forças hidrostáticas:

F R = p c A = ρ g h 2 h w

F R = ρ g w h 2 2

e

y ' = y c + I x x A y c = h 2 + w h 3 12 w h h 2

y ' = 2 h 3

Passo 4

Para a comporta, temos:

- F j a t o ⋅ h j a t o + F R ⋅ h - y ' = 0

F j a t o ⋅ h j a t o = F R ⋅ ( h - y ' )

Substituindo os termos:

u 2 ρ π D 2 4 ⋅ h j a t o = ρ g w h 2 2 ⋅ h - 2 h 3

u 2 ρ π D 2 4 ⋅ h j a t o = ρ g w h 2 2 ⋅ h 3

Isolando u :

u = 2 g w h 3 3 π D 2 h j a t o

Passo 5

Calculando a velocidade V é necessária para que o jato mantenha a comporta na vertical.

Sendo:

g = 9,8   m / s 2 ;

w = 1   m ;

D = 5   c m = 0,05   m ;

h j a t o = 1   m .

Para h = 1   m , temos:

u = 2 ⋅ 9,8 ⋅ 1 ⋅ 1 3 3 ⋅ π ⋅ 0,05 2 ⋅ 1 = 28,8   m / s

Para h = 0,5   m , temos:

u = 2 ⋅ 9,8 ⋅ 1 ⋅ ( 0,5 ) 3 3 ⋅ π ⋅ 0,05 2 ⋅ 1 = 10,2   m / s

Para h = 0,25   m , temos:

u = 2 ⋅ 9,8 ⋅ 1 ⋅ ( 0 , 2 5 ) 3 3 ⋅ π ⋅ 0,05 2 ⋅ 1 = 3,6   m / s

Resposta

28,8   m / s

10,2   m / s

3,6   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere o diagrama do Problema 4.154. Se m = 100k g , ρ = 1000k g / m 3 e A = 0,01m 2 , determine a velocidade V do jato requerida para que o carrinho seja levado ao repouso depois de um segundo se
O regador de gramados mostrado é suprido com água a uma taxa de 68L / m i n . Desprezando o atrito no pivô, determine a velocidade angular do regador em regime permanente para θ = 30 ° . Trace um gráf
O momento é um vetor? Em caso afirmativo, para qual direção ele aponta?
Enuncie o princípio da conservação do momento. O que é possível dizer sobre o momento de um corpo se a força total que age sobre ele é nula?