Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 13.Problemas - Ex. 164
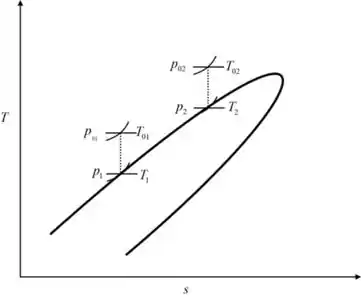
Um combustor de um motor a jato JT8D (como o usado no avião Douglas Dc-9) tem uma vazão mássica de ar de . A área é constante e os efeitos de atrito são desprezíveis. As propriedades na entrada da câmara de combustão são , e . Na saída do combustor, e . O poder calorífico do combustível é ; a razão ar-combustível é grande o suficiente para que as propriedades sejam como as do ar. Calcule a pressão na saída do combustor. Determine a taxa de adição de energia à corrente de ar. Determine a vazão mássica de combustível requerida; compare-a com a vazão mássica de ar. Mostre o processo em um diagrama , indicando os estados de estagnação e estáticos e o caminho do processo.
Passo 1
Calculando a massa específica:
Sendo:
;
;
.
Temos:
Calculando a velocidade do som:
Sendo:
.
Temos:
Calculando :
Sendo:
.
Temos:
Passo 2
Calculando :
Substituindo os dados:
Calculando :
Sendo:
;
.
Temos:
Calculando a taxa de adição de energia:
Sendo:
;
.
Temos:
Passo 3
Calculando a vazão mássica do combustível requerida:
Sendo:
.
Temos:
Comparando com a vazão mássica de ar:
Passo 4
Calculando :
Sendo:
.
Temos:
Passo 5
Demonstrando o processo em um diagrama , indicando os estados de estagnação e estáticos e o caminho do processo:
