Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 13.Problemas - Ex. 162
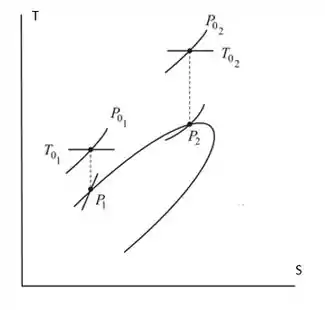
Considere o escoamento sem atrito de ar em um duto de área constante, . Em uma seção, as propriedades estáticas são e e o número de Mach é 0,2. Em uma seção a jusante, a pressão estática é . Desenhe um diagrama mostrando os estudos de estagnação e estáticos. Calcule a velocidade do escoamento e a temperatura na seção a jusante. Avalie a taxa de troca de calor para o processo.
Passo 1
Pelas equações de fluxo de linha Rayleigh:
Sendo:
;
;
;
.
Temos:
Do mesmo modo, calculamos :
Sendo:
.
Temos:
Calculando :
Sendo:
.
Temos:
Passo 2
Calculando :
Substituindo os dados:
Calculando :
Substituindo os dados:
Calculando a vazão mássica:
Sendo:
;
.
Temos:
Calculando a taxa de troca de calor:
Sendo:
.
Temos:
Assim:
Substituindo os dados:
Passo 3
Desenhe um diagrama mostrando os estudos de estagnação e estáticos:
