Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 5.Problemas - Ex. 125

Começando com balanço de energia no elemento de volume na forma de disco, obtenha a equação implícita de diferenças finitas transiente unidimensional para nó geral interno para T ( z , t ) em cilindro cuja superfície lateral é submetida à convecção com coeficiente de convecção h e temperatura ambiente de T ∞ , para o caso de condutividade térmica constante com geração de calor uniforme.

Passo 1

Inicialmente, consideraremos uma vara cilíndrica, na qual tomaremos a sua área de seção transversal, a condutividade térmica e a geração de calor como constantes. Selecionaremos um trecho dessa vara, também em formato cilíndrico, com o mesmo diâmetro da vara completa, e um comprimento de ∆ z , na direção z . Agora, considera-se a condução de calor transiente e unidimensional na direção z desse trecho e temos o nosso objeto de estudo semelhante ao representado abaixo:

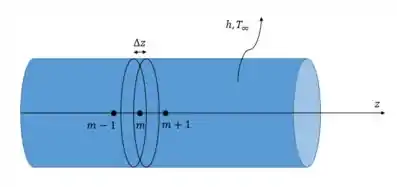
É possível notar que o elemento de volume do nó interior geral envolve a condução de calor de dois lados, convecção na superfície e o volume do elemento é representado por V = A ∆ z , onde A =   π D 2 / 4 . Então, a formulação implícita de diferenças finitas transiente unidimensional pode ser expressa da seguinte maneira:

h p ∆ z T ∞ -   T m i + 1 + k A T m - 1 i + 1 -   T m i + 1 ∆ z + k A T m + 1 i + 1 -   T m i + 1 ∆ z +   e ˙ 0 A ∆ z =   ρ A ∆ z C p T m i + 1 -   T m i ∆ t  

Passo 2

Se multiplicarmos ambos os lados da equação por ∆ z / k A , iremos obter:

h p ∆ z ² k A T ∞ -   T m i + 1 +   T m - 1 i + 1 -   T m i + 1 + T m + 1 i + 1 -   T m i + 1 +   e ˙ 0 A ∆ z ² k =   ρ ∆ z ² C p k ∆ t T m i + 1 -   T m i

E sabendo que a difusividade térmica α = k / ρ C p e τ =   α ∆ t / ∆ z ² , a equação fica dessa forma:

h p ∆ z ² k A T ∞ -   T m i + 1 +   T m - 1 i + 1 +   T m + 1 i + 1 - 2 T m i + 1 +   e ˙ 0 A ∆ z ² k =   T m i + 1 -   T m i τ

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro