Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 2.Problemas - Ex. 65
A comporta AB abaixo é semicircular, articulada em B e mantida por uma força horizontal P em A. Que força P é necessária para o equilíbrio?
Passo 1
Primeira coisa que precisamos entender é que se estamos falando de equilíbrio hidrostático, temos que ter uma força que atua no ponto B de mesma intensidade, direção e módulo que a que atua no ponto A, certo?
O centroide de um semicírculo é dado por . Isso quer dizer que a altura abaixo do ponto P.
Passo 2
Uma vez determinado essa profundidade de atuação da força hidrostática, temos que calculá-la.
Passo 3
A linha de ação de F pode ser calculada também dado que:
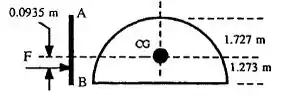
Portanto a força P necessária deve ser igual a força que atua no ponto B.
Resposta
Exercícios de Livros Relacionados
Considere uma superfície curva submersa. Explique como você determinaria a componente horizontal da força hidrostática que age sobre essa superfície.
Considere um contêiner cilíndrico vertical parcialmente preenchido com água. Agora o cilindro é posto a girar com relação a seu eixo a uma velocidade angular especificada, e o movimento de corpo rígid
Uma placa retangular com 4 m de altura e 5 m de largura bloqueia a lateral de um canal de água doce com 4 m de profundidade, como mostra a Figura P3-56. A placa tem dobradiças em tomo de um eixo horiz
Considere dois copos idênticos com água, um parado e o outro se movendo em um plano horizontal com aceleração constante. Considerando que não haja derramamento, qual copo terá a pressão mais alta (a)
Considere um copo com água. Compare as pressões da água na superfície inferior nos seguintes casos: o copo está (a) parado, (b) movendo-se para cima a velocidade constante, (c) movendo-se para baixo a