O comprimento da esteira atrás de um aerofólio é uma função da velocidade do escoamento , do comprimento de corda , da espessura , da massa específica, , e da viscosidade dinâmica, , do fluido. Determine os parâmetros adimensionais que caracterizam este fenômeno.
Passo 1
Oiee, turubom? Nessa questão nós temos a relação funcional entre o comprimento de uma esteira atrás de um aerofólio e outros parâmetros físicos. E com isso queremos encontrar os termos que caracterizam esse fenômeno.
Passo 2
Para resolver essa questão vamos usar o teorema pi de Buckingham. Para o número de parâmetros temos:
![]()
Selecionando as dimensões primárias
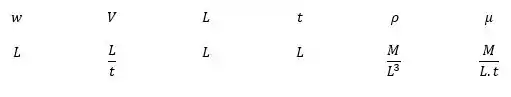
E os parâmetros repetidos:
![]()
Passo 3
Nós temos grupos sem dimensão e configurando as equações dimensionais:
Então,
Somando os expoentes:
Temos que a solução do sistema é:
Então:
Agora vamos conferir se isso está mesmo certinho usando as dimensões :
Passo 4
Para o segundo grupo temos que:
Então,
Somando os expoentes:
Temos que a solução do sistema é:
Então:
Fazendo a conferência usando as dimensões :
Passo 5
Para o terceiro, e último, grupo:
Então,
Somando os expoentes:
Temos que a solução do sistema é:
Então:
Fazendo a conferência usando as dimensões :
Feshow! 😊