Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 10.Problemas - Ex. 98

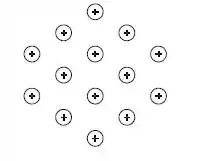
Um condensador de tubos horizontais utilizado para liquefação 900 kg/h de vapor saturado de amônia a 37°C tem 14 tubos de cobre, como mostrado abaixo, cada um com diâmetro interno de 3 cm e externo de 3,8 cm. O refrigerante escoa através dos tubos a uma temperatura média de 20°C, produzindo um coeficiente de transferência de calor de 4,0 kW/m²°K. Para esse condensador, estime (a) o valor médio do coeficiente global de transferência de calor e (b) o comprimento do tubo.

Passo 1

(a) Vamos calcular o que se pede, beleza? Mas temos que lembrar sempre de uma coisa aqui: quando temos vários tubos em horizontal, precisamos calcular o coeficiente de transferência de calor para UM tubo e depois correlacionarmos para vários, se liga!

Mas antes, vamos pegar as propriedades da fase gasosa na temperatura de saturação e a da fase líquida na temperatura de filme!

h f g = 1113 x 10 3 J / k g

ρ v = 11,09   k g / m ³

ρ l = 589   k g / m ³

μ l = 1,303 x 10 - 4   k g / m . s

C P l = 4867   J / k g ° C

K l = 0,4602   W / m . ° C

E aproveitar, calcular o calor latente modificado:

h f g ' = h f g + 0,68 C P l T s a t - T s = 1133 x 10 3   J / k g

h h o r i z o n t a l = 0,729 g ρ l ρ l - ρ v h f g ' K l 3 μ l T s a t - T s D 1 4 = 7693   W / m ² ° C  

Passo 2

Com o coeficiente relacionando pra um tubo, vamos usar essa relação abaixo pra abrangir para N tubos horizontais!

Mas perceba que temos uma fileira com 2 tubos, outra com 3 tubos, outra com 4, 3 e 2

h N   t u b o s   h o r i z o n t a i s = h 1 = h 1   t u b o   h o r i z o n t a l N 1 4 = 7693 2 1 4 = 6469   W / m ² ° C

h 2 = h 1   t u b o   h o r i z o n t a l N 1 4 = 7693 3 1 4 = 5845   W / m ² ° C

h 3 = h 1   t u b o   h o r i z o n t a l N 1 4 = 7693 3 1 4 = 5440   W / m ² ° C

Agora a gente vai fazer uma média desses carinhas aí onde os pesos serão a quantidade de fileiras para cada coeficiente que calculamos!!

h o = 2 x 2 h 1 + 2 x 3 h 2 + 1 x 4 h 3 2 x 2 + 2 x 3 + 1 x 4 = 5908   W / m ² ° C

O primeiro valor representa a quantidade de tubos associado ao coeficiente, enquanto o segundo valor está relacionado ao número de fileiras com aquele número de tubos, por exemplo, 2 x 2h1 = 2 tubos x 2 fileiras!

Passo 3

Vamos agora calcular o coeficiente global de transferência de calor que é

U = D o D i h i + D o ln ⁡ D o D i 2 K + 1 h o - 1 = 0,038 0,03 x 4000 + 0,038 ln ⁡ 3,8 3 2 401 + 1 5908 - 1 = 2012 W m 2 ° C

Passo 4

(b) A gente consegue então agora calcular o comprimento do tubo utilizando a seguinte relação:

q = U A ∆ T = U π D L ∆ T

q = m ˙   h f g = 900 k g h x 1 h 3600 s 1133 x 10 3 = 2,833 x 10 5 W

Agora só a gente isolar o comprimento na equação e ser feliz haha

L = q U π D ∆ T = 2,833 x 10 5 2012 π 0,038 37 - 20 = 4,9   m

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro