Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 2.Problemas - Ex. 41
Condução unidimensional, em regime estacionário e sem geração interna de energia, está ocorrendo em uma parede plana com condutividade térmica constante.
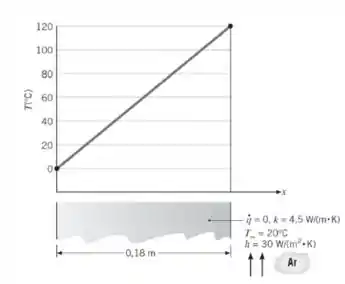
- A distribuição de temperaturas mostrada no gráfico é possível? Explique sucintamente seu raciocínio.
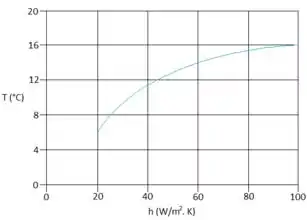
- Com a temperatura em e a temperatura do fluido fixas em e , respectivamente, calcule e represente graficamente a temperatura em , , como uma função de para . Explique sucintamente os seus resultados.
Passo 1
Fala aí! Partiu resolver questõezinhas!
Bom, o nosso enunciado nos dá duas letrinhas para resolver… Pra isso ele nos dá um gráfico de apoio que mostra uma distribuição linear da temperatura em relação a parede, junto com os seguintes dados:
Com esses dados, partiu responder cada letra, beleza?
Passo 2
A letra a, quer saber se essa distribuição linear da temperatura, que o gráfico mostra pra gente, é possível…
Para esse comportamento ser possível tem que válido o seguinte:
Opa! Então vamos fazer essa conta para testar, primeiro com o fluxo de calor de condução:
Agora vamos achar o fluxo de calor na convecção:
Ops! Tem algo aí que não se encaixa, hein?
Olha só:
Não deu zero! Então a distribuição de temperatura do gráfico não é possível!
Passo 3
Agora vamos para a letra b! O nosso enunciado quer que a gente calcule e represente graficamente a temperatura em como uma função de , sabendo que:
Podemos achar a temperatura partindo do mesmo princípio do passo anterior, fazendo assim olha só:
Já que está todo mundo negativo, vamos multiplicar por para facilitar nossos cálculos, ok?
Beleza! Encontramos o ! Agora partiu plotar o gráfico dele em relação ao coeficiente de convecção, vamos nessa?
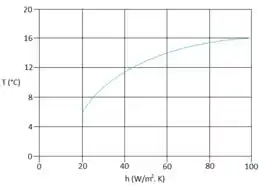
Prontinho! Conseguimos, arrasamos!!
Resposta
- A distribuição de temperatura do gráfico não é possível, pois .
- .
