Em uma camada plana de carvão, com espessura , ocorre geração volumétrica uniforme a uma taxa devido à lenta oxidação de partículas de carvão. Com base em valores médios diários, a superfície superior da camada transfere calor por convecção para o ar ambiente, no qual e , enquanto recebe irradiação solar em uma quantidade . Irradiação a partir da atmosfera pode ser desprezada. A absortividade em relação aos raios solares e a emissividade da superfície são, cada uma, .
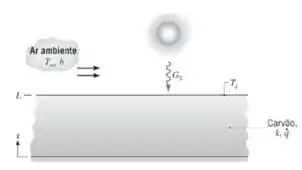
- Escreva a forma para o regime estacionário da equação da difusão térmica para a camada de carvão. Verifique se essa equação é satisfeita pela distribuição de temperaturas com a forma.
- Obtenha uma expressão para a taxa de transferência de calor por condução, por unidade de área, em . Aplicando um balanço de energia em uma superfície de controle ao redor da superfície superior da camada, obtenha uma expressão para . Calcule e para as condições especificadas.
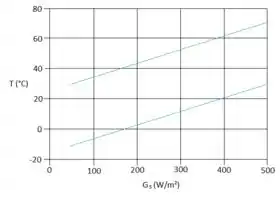
- Os valores médios diários de e dependem de uma série de fatores, tais como o período do ano, nebulosidade e condições do vento. Para , calcule e represente graficamente e em função do valor de para . Para , calcule e represente graficamente e em função de para .
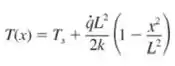
A partir dessa distribuição, o que você pode dizer sobre as condições existentes na superfície inferior ? Esboce a distribuição de temperaturas e aponte suas principais características.
Passo 1
Fala aí! Cara, foca no tamanho dessa questão… Dá até vontade de fugir!

Relaxa! A gente consegue resolver isso juntos!
Bom, o nosso enunciado está dividido em três letrinhas para resolver… Vamos ver cada uma delas com atenção, beleza?
Passo 2
A letra a, pede pra gente a partir da distribuição de temperatura dada por:
Falar sobre as condições existentes na superfície inferior onde: … E além disso pede pra colocar em um gráfico a distribuição de temperatura...
Bom, vamos começar! Se estamos tratando de uma condução unidimensional, podemos usar a equação da difusividade hidráulica:
Olha só, chegamos a conclusão de que para qualquer que seja o valor de a equação é satisfeita, show?
Vamos continuar, pois a letra a ainda não acabou…
Passo 3
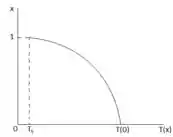
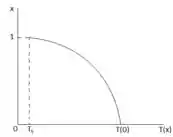
Vamos então plotar o gráfico que nos mostra o comportamento da temperatura com nossos valores de , beleza?
Quando vamos ter: , show?
Vamos ter então:
Passo 4
Agora vamos para a letra b! O nosso enunciado quer que a gente calcule e … Vamos partir do balanço de energia:
ou
Passo 3
Tá faltando encontrar o , então partiu achar ele:
Prontinho! Estamos quase lá! Só falta a última letrinha!
Passo 4
Na letra c, precisamos fazer dois gráficos um que represente e em função do , e outro em função de , sabendo que temos:
Vamos plotar então, sendo a curva azul correspondente a , e a curva verde correspondente a :
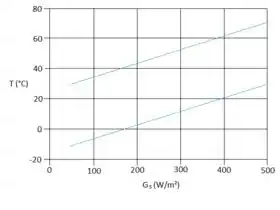
Resposta
- Para qualquer que seja o valor de a equação da difusividade hidráulica é satisfeita.
- e .
-