Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 4.Problemas - Ex. 172
O conjunto carrinho/pá de massa , mostrado no Problema , é movido por um jato de água. A água deixa o bocal estacionário de área , com uma velocidade de . O coeficiente de atrito cinético entre o carrinho e a superfície é . Trace um gráfico da velocidade terminal do conjunto como uma função do ângulo de deflexão da pá, , para . Para qual ângulo, o conjunto começa a mover se o coeficiente de atrito estático é .
Passo 1
Considerações Iniciais:
- Escoamento em estado estacionário;
- Escoamento incompressível;
- Escoamento com velocidade constante ;
- Escoamento uniforme.
Pelas considerações feitas, utilizaremos a seguinte equação da quantidade de movimento:
Passo 2
Analisando em , temos:
Não há resistência, então, :
Não temos a variação das propriedades com o tempo, então:
Assim:
Então:
Sendo:
;
.
Temos:
Passo 3
Analisando em , temos:
Não há resistência, então, :
Não temos a variação das propriedades com o tempo, então:
Assim:
Então:
Sendo:
;
;
.
Temos:
Passo 4
Para temos que e .
Juntaremos as equações do Passo 2 e 3 em uma só:
Passo 5
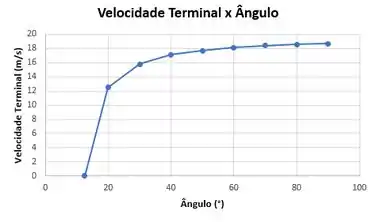
Trace um gráfico da velocidade terminal do conjunto como uma função do ângulo de deflexão da pá.
Sendo:
;
;
;
;
;
.
Temos:
Passo 6
Para qual ângulo, o conjunto começa a mover se o coeficiente de atrito estático é ?
Usando os dados do Passo 5 e com :
Analisando entre e :
Percebemos que o ângulo se aproxima mais de .
Utilizaremos então :
Para o ângulo de 19° o conjunto começa a mover se o coeficiente de atrito estático é .
Resposta
Ângulo de 19°