Considere uma aleta de liga de alumínio de seção transversal triangular cujo comprimento é , espessura da base e largura muito grande na direção normal ao plano do papel. A base da aleta é mantida a uma temperatura de . A aleta perde calor por convecção para o ar ambiente a , com coeficiente de transferência de calor e por radiação para as superfícies envolventes a uma temperatura média de . Usando o método das diferenças finitas com 6 nós igualmente espaçados ao longo da aleta na direção , determine as temperaturas dos nós e a taxa de transferência de calor a partir da aleta para . Considere a emissividade da superfície da aleta como e presuma uma transferência de calor permanente unidimensional na aleta.
Passo 1
Realizando uma representação para facilitar a interpretação do exercício de aleta:
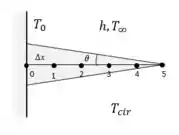
Muito bem! Agora precisamos encontrar o tamanho do nosso elemento finitesimal usando a equação abaixo...
Note que a temperatura no nó 0 equivale a .
Passo 2
Agora vamos aplicar o balanço de energia e encontrar uma equação geral para os nós 1, 2, 3 e 4 que são nós interiores, e claro não podemos nos esquecer que a nossa aleta sofre convecção e radiação:
Observe que esse exercício não se trata de uma aleta de seção retangular, logo ela possuirá áreas diferentes na formulação, como pode se ver na equação acima.
Porém, aqui está umas equações para nos ajudar a encontrar essas áreas...
Beleza, agora podemos substituir essas equações na equação geral.
Que equação enorme né? Para ficar mais prático de fazemos as equações para cada ponto nodal, vamos dividir cada termo por: equações para cada ponto nodal, vamos dividir cada termo por:
Logo ficará assim...
Passo 3
Agora podemos substituir para cada ponto nodal.
E para o nó 5, o nó da extremidade temos a seguinte formulação:
Resolvendo as 5 equações simultaneamente podemos encontrar as seguintes temperaturas:
Passo 4
Para encontrarmos a taxa de transferência de calor para , utilizamos a equação abaixo:
Lembrando que a área de transferência de calor é igual a:
E para os nós da extremidade, ou seja, nó 0 e nó 5:
Com isso temos...
Resultando em...
Resposta
Ei, a resposta está no passo a passo :)