Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 12.Problemas - Ex. 43
Considere o avião hipersônico do Problema 12.35. Quanto tempo levaria para um observador ouvir o avião depois que ele passar sobre o observador? Nesse tempo decorrido, que distância o avião viajou?
Passo 1
Oi pessoal, tudo bem?
Consideremos, do problema 12.35:
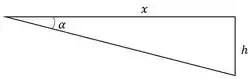
Para o problema, imaginemos que o observador se encontra a x metros do ponto perpendicular à altura do avião, formando um ângulo com o mesmo.
Obs: Propriedades do ar (Tabela A.6). ;
O tempo que leva para voar diretamente de cima para onde você ouve pode ser dado por:
E do esboço realizado, temos:
Passo 2
Sabemos que a velocidade do som:
E que a velocidade do avião depende da velocidade do som, de modo que:
A temperatura equivalente para a altitude dada no problema deve ser encontrada (interpolando) com o auxílio da tabela A.3. Realizando a interpolação, podemos encontrar o valor de , então temos:
Então a velocidade do avião é de:
Passo 3
Como x depende do ângulo de Mach, devemos descobri-lo:
Então:
Por fim, o tempo necessário para um observador ouvir o avião depois que ele passar sobre o observador é de:
Resposta
Portanto: