A temperatura varia linearmente do nível do mar até cerca de 11 km de altitude na atmosfera-padrão. Avalie a taxa de lapso – a taxa de diminuição de temperatura com a altitude – na atmosfera-padrão. Deduza uma expressão para a taxa de variação da velocidade sônica com a altitude em um gás ideal sob condição atmosférica-padrão. Avalie e trace um gráfico para uma faixa de altitude do nível do mar até 10 km.
Passo 1
Oi pessoal, tudo bem?
Consideremos:
Obs: Propriedades do ar (Tabela A.6). ;
Passo 2
Da tabela A.3, podemos encontrar os valores das temperaturas para as altitudes de 0 a 10 km, como mostra a tabela (feita no Excel) a seguir:
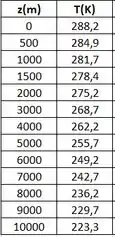
Como a variação da temperatura é linear até a altitude de 11 km, podemos dizer que , então:
Como o problema pede a variação entre 0 e 10 km, a variação m pode ser determinada então como:
Sabemos que a velocidade do som:
Então:
Resposta
Portanto, temos:
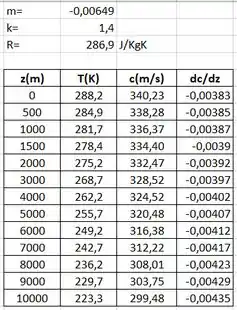
O gráfico então:
