Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 5.Problemas - Ex. 61

Considere um bloco de constante k = 23 W m ∙ K de 5   m de comprimento, 30   c m de altura e 50   c m de largura. O bloco é totalmente submerso em água gelada bem agitada a 0   ° C , e o coeficiente de transferência de calor é tão alto que as temperaturas de ambos os lados do bloco podem ser consideradas 0   ° C . A superfície inferior do bloco está coberta com material de baixa condutividade térmica, de forma que a transferência de calor através da superfície do inferior é desprezível. A superfície superior do bloco é uniformemente aquecida por aquecedor com resistência de 8   k W . Usando o método de diferenças finitas com tamanho da malha de ∆ x = ∆ y = 10   c m e aproveitando da simetria, ( a ) obtenha a formulação de diferenças finitas deste problema para transferência de calor permanente bidimensional, ( b ) determine as temperaturas nodais desconhecidas resolvendo as equações e ( c ) determine a taxa de transferência de calor a partir do bloco para a água gelada.

Passo 1

Primeiramente iremos retirar os dados do enunciado...eu irei colocar aqui pra vocês:

l = 0,1   m ; k = 23 W m ∙ K ; T 0 = 0 ℃ ; Q ˙ 0 = 8000   W ;   ∆ x = ∆ y = 10   c m

Nosso exercício requer uma formulação de diferenças finitas para malha quadrada, logo:

T e s q + T s u p + T d i r + T i n f - 4 T n ó + e ˙ n ó l 2 k = 0

Como não temos geração de calor...

T e s q + T s u p + T d i r + T i n f - 4 T n ó = 0

Além disso utilizando da simetria em nosso exercício de modo a facilitar o cálculo, temos que:

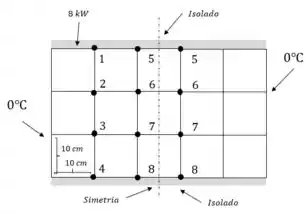
Passo 2

Aplicando nossa fórmula nos 8 nós...

N ó   1 :

q ˙ 0 l + k l 2 T 0 - T 1 l + k l 2 T 5 - T 1 l + k l T 2 - T 1 l = 0

N ó   2 :

T 0 + T 1 + T 3 + T 6 - 4 T 2 = 0

N ó   3 :

T 0 + T 2 + T 4 + T 7 - 4 T 3 = 0

N ó   4 :

T 0 + 2 T 3 + T 8 - 4 T 4 = 0

N ó   5 :

q ˙ 0 l + k l 2 T 1 - T 5 l + k l T 6 - T 5 l + 0 = 0

N ó   6 :

T 2 + T 5 + T 6 + T 7 - 4 T 6 = 0

N ó   7 :

T 3 + T 6 + T 7 + T 8 - 4 T 7 = 0

N ó   8 :

T 4 + 2 T 7 + T 8 - 4 T 8 = 0

Onde,

q ˙ 0 = Q ˙ 0 A = 8000   W 5 × 0,5   m 2 = 3200 W m 2

Passo 3

Resolvendo as 8 equações simultaneamente, podemos chegar nas seguintes temperaturas:

T 1 = 18,2 ° C

T 2 = 9,9 ° C

T 3 = 6,2 ° C

T 4 = 5,2 ° C

T 5 = 25,4 ° C

T 6 = 15,0 ° C

T 7 = 9,9 ° C

T 8 = 8,3 ° C

Passo 4

A taxa de transferência de calor do bloco para a água gelada é de 8   k W , pois todo o calor fornecido ao bloco a partir do topo deve ser igual ao calor transferido do bloco.

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro