Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 5.Problemas - Ex. 83

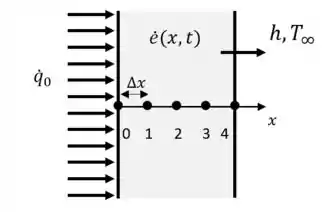
Considere a condução de calor transiente em uma parede plana com geração de calor variável e condutividade térmica constante. A rede nodal do meio consiste dos nós 0, 1, 2, 3 e 4, com espaçamento nodal uniforme de ∆ x . A parede está inicialmente em uma temperatura especificada. Usando a abordagem do balanço de energia, obtenha a formulação explícita de diferenças finitas dos nós de contorno para o caso de fluxo de calor uniforme q ˙ 0 no contorno da esquerda (nó 0) e convecção no contorno da direita (nó 4) com coeficiente de convecção h e temperatura ambiente de T ∞ . Não simplifique.

Passo 1

A partir do enunciado e da figura podemos identificar todos os dados. Temos geração de calor variável e condutividade térmica constante. Note também que há fluxo de calor uniforme q ˙ 0 no contorno da esquerda e convecção no contorno da direita.

Passo 2

Usando a abordagem de balanço de energia nos contornos utilizando o método explícito, temos que:

C o n t o r n o   e s q u e r d o :

k A T 1 i - T 0 i ∆ x + q ˙ 0 A + e ˙ 0 i A ∆ x 2 = ρ A ∆ x 2 c p T 0 i + 1 - T 0 i ∆ t

C O n t r o n o   d i r e i t o :

k A T 3 i - T 4 i ∆ x + h A T ∞ i - T 4 i + e ˙ 4 i A ∆ x 2 = ρ A ∆ x 2 c p T 4 i + 1 - T 4 i ∆ t

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro