Considere uma câmara de combustão tubular com de diâmetro. O ar entra no tubo a , e . Combustível com valor de aquecimento de é queimado quando é aspergido no ar. Se o número de saída de Mach é , determine a taxa com a qual o combustível é queimado e a temperatura de saída. Considere a combustão completa e despreze o aumento da vazão em massa devido à massa do combustível.
Passo 1
A questão é sobre um escoamento de Rayleigh de ar por um tubo circular. O ar recebe calor a uma taxa através da queima de um combustível. O problema pede, primeiro, que a gente calcule a temperatura do ar após seu aquecimento. Depois, ele pede que a gente calcule a vazão mássica de combustível que precisa ser queimada para o ar receber de taxa de calor.
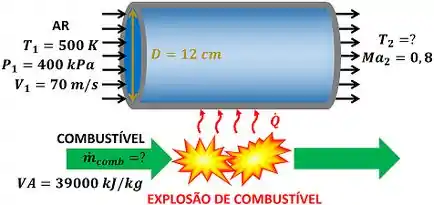
e são as temperaturas do ar antes e depois do aquecimento respectivamente. é a pressão do ar antes do aquecimento. é a velocidade do ar antes do aquecimento. é o número de Mach do ar depois do aquecimento. é o valor de aquecimento do combustível. Ele é basicamente a quantidade de calor que o combustível libera por quilograma .
No próximo passo, vamos entender como calcular a temperatura .
Passo 2
Nós calcularemos a partir da temperatura e usando duas equações. Uma equação que relaciona a temperatura com a temperatura crítica e outra equação que relaciona essa temperatura crítica com a temperatura . Essas duas equações se encontram abaixo.
onde é uma constante que vale para o ar e é o número de Mach do ar antes de ser aquecido.
Invertendo a equação de e multiplicando ela com a equação de , encontramos uma expressão para .
Ainda não sabemos quando vale . No entanto, é obtido através da fórmula do número de Mach.
onde é a velocidade do som no ar antes do ar ser aquecido.
A velocidade do som para um gás ideal é calculada pela fórmula abaixo. Como o ar pode ser considerado um gás ideal, podemos usar a fórmula abaixo para achar .
onde é a constante do ar que vale .
Substituindo os valores em , encontramos:
Usando na equação de :
Por último, substituindo na expressão de , achamos a expressão dessa temperatura.
Passo 3
Esse passo e a primeira parte para calcular a taxa de consumo de combustível suficiente para aquecer o ar até a temperatura .
Para calcular , vamos supor que a taxa de calor liberada pela explosão do combustível é igual à taxa de calor que o ar recebe durante seu escoamento.

A taxa de calor liberada pela explosão do combustível é igual à quantidade de energia por unidade de massa presente no combustível multiplicado pela quantidade de combustível que é queimada a cada segundo .
Além disso, a taxa de calor que o ar recebe é igual à quantidade de calor que o ar recebe por unidade de massa multiplicada pela massa de ar que é aquecida a cada segundo .
Substituindo essa nova equação de na equação anterior, encontramos uma fórmula para .
é a vazão mássica de ar que passa pelo duto. Por isso, ela pode ser calculada pela fórmula da vazão mássica, que multiplica a velocidade do ar pela área por onde o ar passa e pela densidade do ar.
Como o duto é circular com um diâmetro de , pode ser calculada pela expressão da área do círculo.
No entanto, tem que ser convertido antes para metro para usar essa expressão.
Além disso, a densidade pode ser calculada a partir da equação de estado do gás ideal.
Para usar essa equação, convertemos a pressão de para .
Substituindo tudo isso na equação de , achamos:
No próximo passo, aprenderemos a calcular a quantidade de calor que o ar recebe por unidade de massa e encerraremos o cálculo de .
Passo 4
pode ser calculado através da diferença entre a temperatura de estagnação do ar depois de ser aquecido e a temperatura de estagnação do ar antes de ser aquecido .
onde é o calor específico a pressão constante do ar que vale .
pode ser encontrada através da fórmula de temperatura de estagnação abaixo.
Nós calcularemos a partir da temperatura e usando duas equações. Uma equação que relaciona a temperatura com a temperatura crítica e outra equação que relaciona essa temperatura crítica com a temperatura . Essas duas equações se encontram abaixo.
Invertendo a equação de e multiplicando ela com a equação de , encontramos uma expressão para .
Substituindo os dados que temos nessa fórmula, achamos .
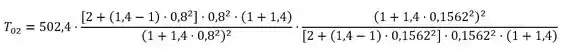
Substituindo esse valor na fórmula de , achamos:
Convertendo de para , ele vira aproximadamente:
Por último, achamos substituindo , na expressão de .