Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 12.Problemas - Ex. 95

Ar é aquecido à medida que escoa de modo subsônico através de um duto. Quando a quantidade de transferência de calor atinge 60   k J / k g , observa-se que o escoamento é estrangulado, e que a velocidade e pressão estática medidas são 620   m / s e 270   k P a . Desprezando as perdas por atrito, determine a velocidade, a temperatura estática e a pressão estática na entrada do duto.

Passo 1

A questão é sobre o escoamento subsônico de Rayleigh de ar. Ou seja, o ar escoa com número de Mach M a 1 < 1 antes de ser aquecido. No entanto, cada quilograma 1   k g de ar que passa pelo duto absorve 60   k J de calor. Isso faz com que o escoamento seja estrangulado. Em outras palavras, após ser aquecido, o ar alcança um número de Mach M a 2 = 1 .

Sabendo disso, a questão quer saber a velocidade V 1 , a pressão P 1 e a temperatura T 1 do ar antes de ser aquecido.

A figura abaixo mostra todos os dados que a questão nos dá e os dados que a questão pede.

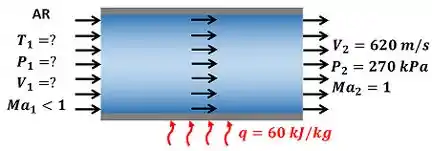
onde V 2 é a velocidade, P 2 é a pressão e M a 2 é o número de Mach do ar depois de ser aquecido. q é a quantidade de calor por unidade de massa transferida para o ar.

A primeira etapa para achar V 1 , P 1 e T 1 é achar M a 1 .

Faremos isso no próximo passo.

Passo 2

Neste passo nós encontraremos o valor do número de Mach do ar antes de ser aquecido M a 1 .

O passo a passo para achar M a 1 é:

  1. Achar a temperatura do ar aquecido T 2 através da equação da velocidade do som c para gás ideal.

    2. c 2 = k R T 2       ⟹       T 2 = c 2 2 k ⋅ R

    onde k é uma constante que vale 1,4 para o ar, R é a constante de gás do ar que vale 287   J / k g e c 2 é a velocidade do som no ar aquecido.

    c 2 é encontrado através da equação do número de Mach M a 2 .

    M a 2 = V 2 c 2       ⟹     c 2 = V 2 M a 2       ⟹       c 2 = 620 1       ⟹       c 2 = 620   m / s

    Substituindo c 2 na equação de T 2 :

    T 2 = c 2 2 k ⋅ R       ⟹       T 2 = 620 2 1,4 ⋅ 287       ⟹       T 2 = 956,7   K

  2. Achar a temperatura de estagnação do ar aquecido T 02 através da equação de temperatura de estagnação de um gás ideal.

    3. T 02 = T 2 + V 2 2 2 c p

    onde c p é o calor específico a pressão constante do ar. Ele vale 1,005   k J / k g ou 1005   J / k g .

    Substituindo c p , achamos T 02 .

    T 02 = T 2 + V 2 2 2 c p       ⟹       T 02 = 956,7 + 620 2 2 ⋅ 1005       ⟹       T 02 = 1147,9   K

  3. Achar a temperatura de estagnação do ar que ainda não foi aquecido T 01 através da equação de q . Atenção, dessa vez devemos usar o valor de c p em k J / k g K , porque q é dado em k J / k g .

    4. q = c p ⋅ T 02 - T 01     ⟹     T 01 = T 02 - q c p     ⟹     T 01 = 1147,9 - 60 1,005

    T 01 = 1088,2   K

  4. Achar o valor da temperatura crítica de estagnação T 0 * , encontrando o valor de T 02 / T 0 * para o número de Mach M a 2 = 1 através da tabela A-15 do livro.

    5. T 02 T 0 * = v a l o r   t a b e l a d o       ⟹       T 0 * = T 02 v a l o r   t a b e l a d o

    Esse valor tabelado está na mesma linha de M a = 1 e na mesma coluna de T 0 / T 0 * as tabela A-15. Logo, a razão de temperaturas vale:

    v a l o r   t a b e l a d o = 1

    Substituindo isso na equação de T 0 * , achamos:

    T 0 * = T 02 v a l o r   t a b e l a d o     ⟹     T 0 * = 1147,9 1     ⟹     T 0 * = 1147,9   K

  5. Achar o valor do número de Mach M a 1 na tabela A-15 do livro para um determinado valor de T 01 / T 0 * . Ou seja, nós faremos o oposto do que fizemos na etapa anterior. Antes, achamos um valor tabelado de T 02 / T 0 * para um valor de M a 2 = 1 . Agora, vamos achar um valor tabelado de M a 1 para um valor de T 01 / T 0 * .

T 01 T 0 * = 1088,2 1147,9       ⟹       T 01 T 0 * = 0,9480

O T 0 T 0 * que temos está entre dois valores de T 0 T 0 * da tabela: T 0 T 0 * = 0,9085 e T 0 T 0 * = 0,9639 . Ou seja, o número de Mach M a 1 está entre dois números de Mach: M a = 0,7 relativo a T 0 T 0 * = 0,9085 e M a = 0,8 relativo a T 0 T 0 * = 0,9639 . Para achar M a para o valor de T 0 T 0 * que queremos, teremos que interpolar!

M a 1 = 0,7 + 0,8 - 0,7 0,9639 - 0,9085 ⋅ 0,9480 - 0,9085     ⟹       M a 1 = 0,771

Passo 3

Nesse passo, calcularemos T 1 . Acharemos esse valor através da tabela A-15 do livro. Os passo a passos para achar V 1 , P 1 e T 1 são muito parecidos entre si. Logo, entendemos o passo a passo de T 1 , entenderemos o passo a passo de V 1 e P 1 .

O passo a passo para achar T 1 se encontra abaixo.

  1. Primeiro, encontramos o valor de T 1 / T * (onde T * é a temperatura crítica) para M a 1 = 0,771 na tabela A-15. T 1 / T * está na mesma linha de M a 1 = 0,771 e na mesma coluna que T / T * . O problema é que não existe uma linha onde M a 1 = 0,7 71 . O valor de M a 1 = 0,7 71 que temos está entre dois valores de M a da tabela:

    2. M a = 0,7 < M a 1 = 0,771 < M a = 0,8

    Ou seja, o valor de T 1 / T * que queremos está entre dois valores de T / T * : T T * = 0,9929 para M a = 0,7 e T T * = 1,0255 para M a = 0,8 . Para achar M a para o valor de T T * que queremos, teremos que interpolar!

    T 1 T * = 0,9929 + 1,0255 - 0,9929 0,8 - 0,7 ⋅ 0,771 - 0,7       ⟹       T 1 T * = 1,0160

  2. Depois, achamos o valor de T 2 / T * para M a 2 = 1 na tabela A-15. T 2 / T * está na mesma linha de M a 2 = 1 e na mesma coluna que T / T * .

    3. T 2 T * = 1,0

  3. Agora, nós invertemos T 2 / T * T 2 T * - 1 = T * T 2 e multiplicamos por T 1 / T * . Isso vai fazer o T * sumir e acharemos uma expressão para T 1 .

T * T 2 ⋅ T 1 T * = 1 1,0 ⋅ 1,0160       ⟹   T 1 956,7 = 1,0160       ⟹       T 1 = 1,0160 ⋅ 956,7

T 1 = 972,0   K

Passo 4

Nesse passo, calcularemos P 1 . O passo a passo para achar P 1 é muito parecido com o passo a passo para achar T 1

  1. Primeiro, encontramos o valor de P 1 / P * (onde P * é a pressão crítica) para M a 1 = 0,771 na tabela A-15. P 1 / P * está na mesma linha de M a 1 = 0,771 e na mesma coluna que P / P * . O problema é que não existe uma linha onde M a 1 = 0,7 71 . O valor de M a 1 = 0,7 71 que temos está entre dois valores de M a da tabela:

    2. M a = 0,7 < M a 1 = 0,771 < M a = 0,8

    Ou seja, o valor de P 1 / P * que queremos está entre dois valores de P / P * : P P * = 1,4235 para M a = 0,7 e P P * = 1,2658 para M a = 0,8 . Para achar M a para o valor de P P * que queremos, teremos que interpolar!

    P 1 P * = 1,4235 + 1,2658 - 1,4235 0,8 - 0,7 ⋅ 0,771 - 0,7       ⟹       P 1 P * = 1 , 3115

  2. Depois, achamos o valor de P 2 / P * para M a 2 = 1 na tabela A-15. P 2 / P * está na mesma linha de M a 2 = 1 e na mesma coluna que P / P * .

    3. P 2 P * = 1,0

  3. Agora, nós invertemos P 2 / P * P 2 P * - 1 = P * P 2 e multiplicamos por P 1 / P * . Isso vai fazer P * sumir e acharemos uma expressão para P 1 .

P * P 2 ⋅ P 1 P * = 1 1,0 ⋅ 1 , 3115       ⟹   P 1 270 = 1 , 3115       ⟹       P 1 = 1 , 3115 ⋅ 270

P 1 = 354   k P a

Passo 5

Nesse passo, calcularemos V 1 . O passo a passo para achar V 1 é muito parecido com o passo a passo para achar P 1 e T 1

  1. Primeiro, encontramos o valor de V 1 / V * (onde V * é a velocidade crítica) para M a 1 = 0,771 na tabela A-15. V 1 / V * está na mesma linha de M a 1 = 0,771 e na mesma coluna que V / V * . O problema é que não existe uma linha onde M a 1 = 0,7 71 . O valor de M a 1 = 0,7 71 que temos está entre dois valores de M a da tabela:

    2. M a = 0,7 < M a 1 = 0,771 < M a = 0,8

    Ou seja, o valor de V 1 / V * que queremos está entre dois valores de V / V * : V V * = 0,6975 para M a = 0,7 e V V * = 0,8101 para M a = 0,8 . Para achar M a para o valor de V V * que queremos, teremos que interpolar!

    V 1 V * = 0,6975 + 0,8101 - 0,6975 0,8 - 0,7 ⋅ 0,771 - 0,7       ⟹       V 1 V * = 0 , 777 4

  2. Depois, achamos o valor de V 2 / V * para M a 2 = 1 na tabela A-15. V 2 / V * está na mesma linha de M a 2 = 1 e na mesma coluna que V / V * .

    3. V 2 V * = 1,0

  3. Agora, nós invertemos V 2 / V * V 2 V * - 1 = V * V 2 e multiplicamos por V 1 / V * . Isso vai fazer V * sumir e acharemos uma expressão para V 1 .

V * V 2 ⋅ V 1 V * = 1 1,0 ⋅ 0 , 777 4       ⟹   V 1 620 = 0 , 777 4       ⟹       V 1 = 0 , 777 4 ⋅ 62 0

V 1 = 482   m / s

Resposta

T 1 = 972,0   K

P 1 = 354   k P a

V 1 = 482   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Água a 15 ° C escoa a uma profundidade de 0,4m com velocidade média de 6m / s em um canal retangular Determine (a) a profundidade crítica, (b) a profundidade alternativa e (c) a energia mínima específ
Considere um canal de água com diâmetro interno de 1m feito de concreto polido ( n = 0,012 ) . A inclinação do canal é 0,002 . Para uma profundidade de escoamento de 0,25m no centro, determine a vazão
Um canal de água de ferro fundido em forma de V mostrado na Figura P13-55 tem uma inclinação do fundo de 0,5 ° . Para uma profundidade de escoamento de 1m no centro, determine a taxa de descarga no es
Repita o Problema 13-53 para um canal de terra escavado coberto de vegetação com n =0,030 .
Reconsidere o Problema 13-50. Se a altura máxima de escoamento que o canal consegue acomodar é 2,4m , determine a vazão máxima de escoamento através do canal.