Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 5.Problemas - Ex. 33

Considere uma colher de aço inoxidável ( k = 15,1 W m ∙ K ,   ε = 0,6 ) parcialmente submersa na água em ebulição a 100 ° C em uma cozinha a 32 ° C . A alça da colher tem seção transversal de cerca de 0,2 c m × 1   c m e estende-se 18   c m ao ar livre a partir da superfície da água. A colher perde calor por convecção para o ar ambiente, com coeficiente médio de transferência de calor h = 13 W m 2 ∙ K , assim como por radiação para as superfícies ao redor a uma temperatura média de T c i r = 295   K . Pressupondo uma transferência de calor permanente unidimensional ao longo da colher e um espaçamento nodal de 3   c m , (a) obtenha a formulação de diferenças finitas de todos os nós, ( b ) determine a temperatura da ponta da colher, resolvendo essas equações, e ( c ) determine a taxa de transferência de calor a partir da superfície exposta da colher.

Passo 1

A partir do espaçamento nodal dado pelo exercício, nós podemos encontrar o número de pontos nodais...

M = L ∆ x + 1 = 18   c m 3   c m + 1 = 7

Agora podemos fazer uma representação do problema:

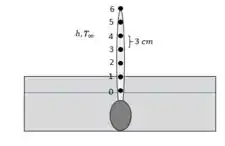
Note que o nosso nó 0 equivale a nossa T 0 = 100 ° C .

Formulando a equação de diferenças finitas para os nossos pontos interiores 1, 2, 3, 4 e 5 temos...

k A T m - 1 - T m ∆ x + k A T m + 1 - T m ∆ x + h p ∆ x T ∞ - T m + ε σ p ∆ x T c i r 4 - T m + 273 4 = 0

Dividindo todos os termos por k A ∆ x :

T m - 1 - 2 T m + T m + 1 + h p ∆ x 2 k A T ∞ - T m + ε σ p ∆ x 2 k A T c i r 4 - T m + 273 4 = 0

Onde,

A = 1   c m 0,2   c m = 0,2   c m 2 = 0,2 × 10 - 4 m 2

p = 2 1 + 0,2   c m = 2,4   c m = 0,024   m

Passo 2

Agora que temos uma equação geral, basta aplicarmos em cada ponto nodal.

Para o N ó   1 :

T 0 - 2 T 1 + T 2 + h p ∆ x 2 k A T ∞ - T 1 + ε σ p ∆ x 2 k A T c i r 4 - T 1 + 273 4 = 0

Para o N ó   2 :

T 1 - 2 T 2 + T 3 + h p ∆ x 2 k A T ∞ - T 2 + ε σ p ∆ x 2 k A T c i r 4 - T 2 + 273 4 = 0

Para o N ó   3 :

T 2 - 2 T 3 + T 4 + h p ∆ x 2 k A T ∞ - T 3 + ε σ p ∆ x 2 k A T c i r 4 - T 3 + 273 4 = 0

Para o N ó   4 :

T 3 - 2 T 4 + T 5 + h p ∆ x 2 k A T ∞ - T 4 + ε σ p ∆ x 2 k A T c i r 4 - T 4 + 273 4 = 0

Para o N ó   5 :

T 4 - 2 T 5 + T 6 + h p ∆ x 2 k A T ∞ - T 5 + ε σ p ∆ x 2 k A T c i r 4 - T 5 + 273 4 = 0

E para o nosso N ó   6 , ou seja, o nó da extremidade, aplicando o balanço de energia fica assim:

k A T 5 - T 6 ∆ x + h p ∆ x 2 + A T ∞ - T 6 + ε σ p ∆ x 2 + A T c i r 4 - T 6 + 273 4 = 0

Passo 3

Resolvendo as equações encontradas simultaneamente, chegaremos nessas temperaturas...

T 1 = 54,1 ° C

T 2 = 38,3 ° C

T 3 = 32,8 C

T 4 = 30,9 C

T 5 = 30,2 ° C

T 6 = 30,1 ° C

Passo 4

Com as temperaturas encontradas, nós podemos usar a equação a baixo para obtermos a taxa de transferência de calor.

Q ˙ a l e t a = ∑ m = 0 6 Q ˙ e l e m e n t o ,   m = ∑ m = 0 6 h A s u p e r f í c i e ,   m T m - T ∞ + ∑ m = 0 6 ε σ A s u p e r f í c i e ,   m T m + 273 4 - T c i r 4

Onde para o N ó   0 :

A s u p e r f í c i e ,   m = p ∆ x 2

Para o N ó   6 :

A s u p e r f í c i e ,   m = p ∆ x 2 + A

Para os N ó s   1 ,   2 ,   3 ,   4 e 5 :

A s u p e r f í c i e ,   m = p ∆ x

Portanto, para finalizar...

Q ˙ a l e t a = 0,92 W

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro